某建设工程准备招标,指挥部现接到甲、乙两个工程队的投标书,从投标书中得知:乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍;该工程若由甲队先做6天,剩下的工程再由甲、乙两队合作16天可以完成.
(1)求甲、乙两队单独完成这项工程各需要多少天?
(2)已知甲队每天的施工费用为0.67万元,乙队每天的施工费用为0.33万元,该工程预算的施工费用为19万元.为缩短工期,拟安排甲、乙两队同时开工合作完成这项工程,问:该工程预算的施工费用是否够用?若不够用,需要追加预算多少万元?请说明理由.
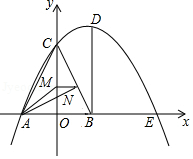
如图,抛物线 与坐标轴分别交于点 , , 三点,其中 , ,点 在 轴上, ,过点 作 轴交抛物线于点 ,点 , 分别是线段 , 上的动点,且 ,连接 , , .
(1)求抛物线的解析式及点 的坐标;
(2)当 是直角三角形时,求点 的坐标;
(3)试求出 的最小值.
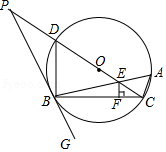
如图, 内接于 , , 为直径, 与 相交于点 ,过点 作 ,垂足为 ,延长 交 的延长线于点 ,连接 .
(1)求证: 与 相切;
(2)若 ,求 的值;
(3)在(2)的条件下,若 的半径为8, ,求 的长.
某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的 ,乙仓库所存原料的 ,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元 吨和100元 吨.经协商,从甲仓库到工厂的运价可优惠 元 吨 ,从乙仓库到工厂的运价不变,设从甲仓库运 吨原料到工厂,请求出总运费 关于 的函数解析式(不要求写出 的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着 的增大, 的变化情况.
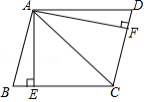
如图,在 中, , ,垂足分别为 , ,且 .
(1)求证: 是菱形;
(2)若 , ,求 的面积.
某市将开展以“走进中国数学史”为主题的知识竞赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按 , , , 四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
|
成绩等级 |
频数(人数) |
频率 |
|
|
4 |
0.04 |
|
|
|
0.51 |
|
|
|
|
|
|
||
|
合计 |
100 |
1 |
(1)求 , ;
(2)在扇形统计图中,求“ 等级”所对应圆心角的度数;
(3)成绩等级为 的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.