现有5名男生和3名女生.
(1)若3名女生必须相邻排在一起,则这8人站成一排,共有多少种不同的排法?
(2)若从中选5人,且要求女生只有2名, 站成一排,共有多少种不同的排法?
(本小题满分12分)
已知圆C: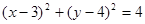 ,直线
,直线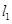 过定点A (1,0).
过定点A (1,0).
(1)若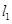 与圆C相切,求
与圆C相切,求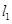 的方程;
的方程;
(2)若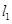 与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线
与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线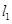 的方程.
的方程.
(本小题满分12分)
已知数列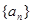 的前
的前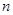 项和
项和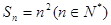 ,数列
,数列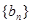 为等比数列,且满足
为等比数列,且满足 ,
,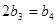
(1)求数列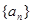 ,
,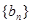 的通项公式;
的通项公式;
(2)求数列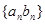 的前
的前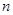 项和。
项和。
(本小题满分12分)
已知函数 .
.
(1)将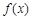 写成
写成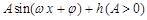 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(2)如果△ABC的三边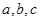 依次成等比数列,且边
依次成等比数列,且边 所对的角为
所对的角为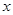 ,试求
,试求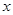 的取值范围及此时函数
的取值范围及此时函数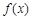 的值域.
的值域.
(本小题满分10分). 选修4-5:不等式选讲
已知函数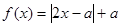 .
.
(1)若不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(2)在(1)的条件下,若存在实数 使
使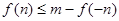 成立,求实数
成立,求实数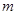 的取值范围.
的取值范围.
(本小题满分10分) 选修4-4:坐标系与参数方程
在直角坐标系 中, 过点
中, 过点 作倾斜角为
作倾斜角为 的直线
的直线 与曲线
与曲线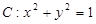 相交于不同的两点
相交于不同的两点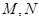 .
.
(1) 写出直线 的参数方程;
的参数方程;
(2) 求 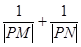 的取值范围.
的取值范围.