在平面直角坐标系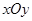 中,点
中,点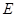 到两点
到两点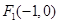 ,
, 的距离之和为
的距离之和为 ,设点
,设点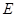 的轨迹为曲线
的轨迹为曲线 .
.
(1)写出 的方程;
的方程;
(2)设过点 的斜率为
的斜率为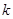 (
( )的直线
)的直线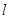 与曲线
与曲线 交于不同的两点
交于不同的两点 ,
,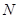 ,点
,点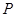 在
在 轴上,且
轴上,且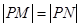 ,求点
,求点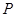 纵坐标的取值范围.
纵坐标的取值范围.
如图,在四棱锥 中,底面
中,底面 为菱形,其中
为菱形,其中 ,
, .
.
(1)求证:
(2)若平面 平面
平面 ,求二面角
,求二面角 的正切值.
的正切值.
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,
求数学成绩在[50,90)之外的人数.
| 分数段 |
[50,60) |
[60, 70) |
[70,80) |
[80,90) |
| x∶y |
1∶1 |
2∶1 |
3∶4 |
4∶5 |
将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为5的概率;
(2)两数中至少有一个奇数的概率.
已知命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立;命题q:函数f(x)=-(5-2a)x是减函数,若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
已知双曲线 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率
轴上,离心率 ,虚轴长为2.
,虚轴长为2.
(1)求双曲线 的标准方程;
的标准方程;
(2)若直线 与双曲线
与双曲线 相交于
相交于 两点,(
两点,( 均异于左、右顶点),且以
均异于左、右顶点),且以 为直径的圆过双曲线
为直径的圆过双曲线 的左顶点
的左顶点 ,求证:直线
,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.