在极坐标系内,已知曲线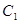 的方程为
的方程为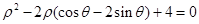 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线 的参数方程为
的参数方程为 (
(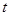 为参数).
为参数).
(1)求曲线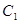 的直角坐标方程以及曲线
的直角坐标方程以及曲线 的普通方程;
的普通方程;
(2)设点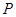 为曲线
为曲线 上的动点,过点
上的动点,过点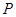 作曲线
作曲线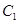 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
求证:(1) ;
;
(2)AB2=BE•BD-AE•AC.
已知椭圆 左、右焦点分别为F1、F2,点
左、右焦点分别为F1、F2,点 ,点F2在线段PF1的中垂线上.
,点F2在线段PF1的中垂线上.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为
与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为 ,且
,且 ,求证:直线
,求证:直线 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
设数列
(1)求
|
(2)求 的表达式.
的表达式.
如图所示的多面体,它的正视图为直角三角形,侧视图为矩形,俯视图为直角梯形(尺寸如图所示)
(1)求证:AE//平面DCF;
(2)当AB的长为 ,
, 时,求二面角A—EF—C的大小.
时,求二面角A—EF—C的大小.
甲、乙两人同时参加奥运志愿者的选拔赛,已知在备选的10道题中,甲能答对其中的6题,乙能答对其中的8题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才能入选.
(1)求甲答对试题数 的分布列及数学期望;
的分布列及数学期望;
(2)求甲、乙两人至少有一人入选的概率.