甲、乙两人同时参加奥运志愿者的选拔赛,已知在备选的10道题中,甲能答对其中的6题,乙能答对其中的8题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才能入选.
(1)求甲答对试题数 的分布列及数学期望;
的分布列及数学期望;
(2)求甲、乙两人至少有一人入选的概率.
(本小题满分14分)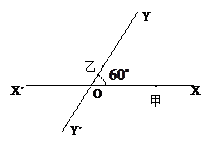
如图,有两条相交成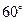 的直路
的直路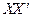 ,
,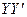 ,交点是
,交点是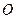 ,甲、乙分别在
,甲、乙分别在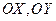 上,起初甲离O点3 km,乙离O点1 km,后甲沿
上,起初甲离O点3 km,乙离O点1 km,后甲沿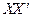 方向用2 km/h的速度,乙沿
方向用2 km/h的速度,乙沿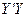 方向用4km/h的速度同时步行. 设t小时后甲在
方向用4km/h的速度同时步行. 设t小时后甲在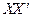 上点A处,乙在
上点A处,乙在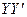 上点B处.
上点B处.
(Ⅰ)求t=1.5时,甲、乙两人之间的距离;
(Ⅱ)求t=2时,甲、乙两人之间的距离;
(Ⅲ) 当t为何值时,甲、乙两人之间的距离最短?
(本小题满分14分)
为了检测某种产品的直径(单位mm),抽取了一个容量为100的样本,其频率分布表(不完整)如下:
| 分组 |
频数累计 |
频数 |
频率 |
| [10.75,10.85) |
6 |
6 |
0.06 |
| [10.85,10.95) |
15 |
9 |
0.09 |
| [10.95,11.05) |
30 |
15 |
0.15 |
| [11.05,11.15) |
48 |
18 |
0.18 |
| [11.15,11.25) |
▲ |
▲ |
▲ |
| [11.25,11.35) |
84 |
12 |
0.12 |
| [11.35,11.45) |
92 |
8 |
0.08 |
| [11.45,11.55) |
98 |
6 |
0.06 |
| [11.55,11.65) |
100 |
2 |
0.02 |
(Ⅰ)完成频率分布表;
(Ⅱ)画出频率分布直方图;
(Ⅲ)据上述图表,估计产品直径落在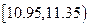 范围内的可能性是百分之几?
范围内的可能性是百分之几?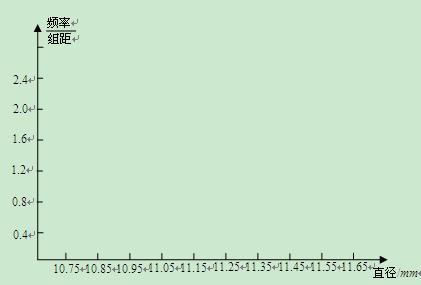
(本小题满分14分)
一只袋中装有2个白球、3个红球,这些球除颜色外都相同。
(Ⅰ)从袋中任意摸出1个球,求摸到的球是白球的概率;
(Ⅱ)从袋中任意摸出2个球,求摸出的两个球都是白球的概率;
(Ⅲ)从袋中任意摸出2个球,求摸出的两个球颜色不同的概率。
(本小题满分10分)
如图,四面体ABCD中,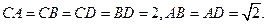
(1)求证:平面ABD⊥平面BCD;
(2)求异面直线AB与CD所成角的余弦值。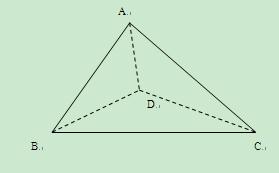
(本小题满分10分)
已知圆 ,直线
,直线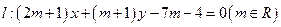 。
。
(1)求证直线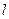 恒过定点,并求出该定点;
恒过定点,并求出该定点;
(2)当直线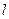 被圆
被圆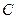 截得弦长最小时,求此时直线
截得弦长最小时,求此时直线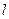 的方程。
的方程。