(本小题满分14分)
一只袋中装有2个白球、3个红球,这些球除颜色外都相同。
(Ⅰ)从袋中任意摸出1个球,求摸到的球是白球的概率;
(Ⅱ)从袋中任意摸出2个球,求摸出的两个球都是白球的概率;
(Ⅲ)从袋中任意摸出2个球,求摸出的两个球颜色不同的概率。
已知椭圆 (
( >
> >0)的离心率
>0)的离心率 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设直线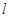 与椭圆相交于不同的两点
与椭圆相交于不同的两点 ,已知点
,已知点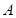 的坐标为(
的坐标为(  ,0),点
,0),点 (0,
(0,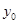 )在线段
)在线段 的垂直平分线上,且
的垂直平分线上,且 ,求
,求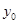 的值.
的值.
在数列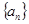 和
和 中,已知
中,已知 .
.
(1)求数列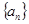 和
和 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列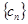 的前n项和
的前n项和 .
.
已知四棱锥 的底面
的底面 是等腰梯形,
是等腰梯形, 且
且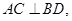


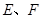 分别是
分别是 的中点.
的中点.
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
已知向量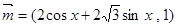 ,
, ,且
,且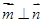 .
.
(1)将 表示为
表示为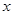 的函数
的函数 ,并求
,并求 的单调递增区间;
的单调递增区间;
(2)已知 分别为
分别为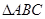 的三个内角
的三个内角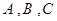 对应的边长,若
对应的边长,若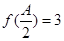 ,且
,且 ,
,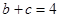 ,求
,求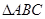 的面积.
的面积.
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意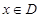 ,存在常数
,存在常数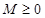 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的一个上界.已知函数
的一个上界.已知函数 ,
, .
.
(1)若函数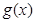 为奇函数,求实数
为奇函数,求实数 的值;
的值;
(2)在(1)的条件下,求函数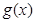 在区间
在区间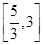 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数 在
在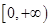 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围.
的取值范围.