定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意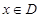 ,存在常数
,存在常数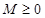 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的一个上界.已知函数
的一个上界.已知函数 ,
, .
.
(1)若函数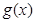 为奇函数,求实数
为奇函数,求实数 的值;
的值;
(2)在(1)的条件下,求函数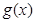 在区间
在区间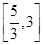 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数 在
在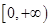 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围.
的取值范围.
如图,正方体ABCD-A1B1C1D1的棱长为8cm,M、N、P分别是AB、A1D1、BB1的中点;(1)画出过M、N、P三点的平面与平面A1B1C1D1的交线以及与平面BB1C1C的交线;(2)设过M、N、P三点的平面与B1C1交于点Q,求PQ的长; 
在三棱锥A-BCD中,E、F分别是线段AD、BC上的点,满足 ,AB=CD=3,且AB与CD所成的角为60o,求EF的长.
,AB=CD=3,且AB与CD所成的角为60o,求EF的长.
矩形ABCD(AB≤BC)中,AC=2 ,沿对角线AC把它折成直二面角B-AC-D后,BD=
,沿对角线AC把它折成直二面角B-AC-D后,BD= ,求AB、BC的长.
,求AB、BC的长.
 |
翰林汇
已知数列{an}满足a1=2,对于任意的n∈N,都有an>0,且(n+1)a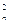 +anan+1-na
+anan+1-na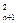 =0,又知数列{bn}:b1=2n-1+1
=0,又知数列{bn}:b1=2n-1+1
(1)求数列{an}的通项an以及它的前n项和Sn;
(2)求数列{bn}的前n项和Tn;
(3)猜想Sn和Tn的大小关系,并说明理由.
如图,平行六面体ABCD-A'B'C'D'中,AC=2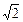 ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
(1)求侧棱AA'与底面ABCD所成角的大小;
(2)求侧面A'ADD'底面ABCD所成二面角的正切值;
(3)求四棱锥C-A'ADD'的体积.