(本小题满分14分)
为了检测某种产品的直径(单位mm),抽取了一个容量为100的样本,其频率分布表(不完整)如下:
| 分组 |
频数累计 |
频数 |
频率 |
| [10.75,10.85) |
6 |
6 |
0.06 |
| [10.85,10.95) |
15 |
9 |
0.09 |
| [10.95,11.05) |
30 |
15 |
0.15 |
| [11.05,11.15) |
48 |
18 |
0.18 |
| [11.15,11.25) |
▲ |
▲ |
▲ |
| [11.25,11.35) |
84 |
12 |
0.12 |
| [11.35,11.45) |
92 |
8 |
0.08 |
| [11.45,11.55) |
98 |
6 |
0.06 |
| [11.55,11.65) |
100 |
2 |
0.02 |
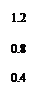
(Ⅰ)完成频率分布表;
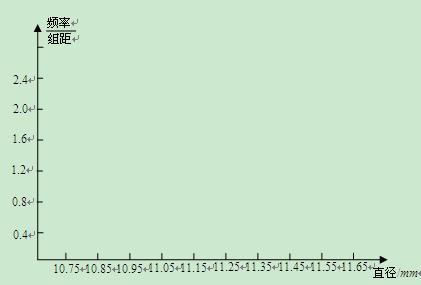
(Ⅱ)画出频率分布直方图;
(Ⅲ)据上述图表,估计产品直径落在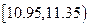 范围内的可能性是百分之几?
范围内的可能性是百分之几?
解关于 的不等式:
的不等式:
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC.
(1)求角C的大小;
(2)求 的最大值,并求取得最大值时角A、B的大小.
的最大值,并求取得最大值时角A、B的大小.
本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知 的三个顶点在抛物线
的三个顶点在抛物线 :
: 上运动,
上运动,
(1). 求 的焦点坐标;
的焦点坐标;
(2). 若点 在坐标原点, 且
在坐标原点, 且 ,点
,点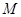 在
在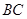 上,且
上,且 ,
,
求点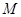 的轨迹方程;
的轨迹方程;
(3). 试研究: 是否存在一条边所在直线的斜率为 的正三角形
的正三角形 ,若存在,求出这个正三角形
,若存在,求出这个正三角形 的边长,若不存在,说明理由.
的边长,若不存在,说明理由.
本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小
题满分7分.
已知函数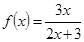 ,数列
,数列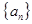 满足
满足 ,
, ,
,
(1). 求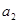 ,
,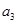 ,
, 的值;
的值;
(2). 求证:数列 是等差数列;
是等差数列;
(3). 设数列 满足
满足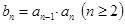 ,
,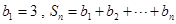 ,
,
若 对一切
对一切 成立,求最小正整数
成立,求最小正整数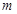 的值.
的值.
本题共有2个小题,第1小题满分6分,第2小题满分8分.
若函数 ,如果存在给定的实数对
,如果存在给定的实数对 ,使得
,使得
恒成立,则称 为“
为“ 函数” .
函数” .
(1). 判断下列函数,是否为“ 函数”,并说明理由;
函数”,并说明理由;
① ②
② 
(2). 已知函数 是一个“
是一个“ 函数”,求出所有的有序实数对
函数”,求出所有的有序实数对 .
.