为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的 、 、 ,现在3名工人独立地从中任选一个项目参与建设。
(1)求他们选择的项目所属类别互不相同的概率;
(2)记 为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求 的分布列及数学期望。
(本小题满分10分)
椭圆C: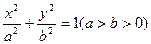 的两个焦点为
的两个焦点为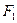 、
、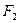 ,点
,点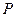 在椭圆C上,且
在椭圆C上,且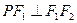 ,
,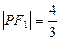 ,
,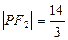 .
.
(1) 求椭圆C的方程;
(2) 若直线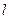 过圆
过圆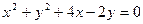 的圆心
的圆心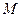 ,交椭圆C于
,交椭圆C于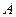 、
、 两点,且
两点,且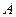 、
、 关于点
关于点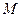 对称,求直线
对称,求直线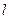 的方程.
的方程.
(本小题满分12分)
已知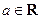 ,函数
,函数 .
.
(1)若函数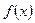 在区间
在区间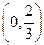 内是减函数,求实数
内是减函数,求实数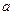 的取值范围;
的取值范围;
(2)求函数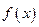 在区间
在区间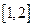 上的最小值
上的最小值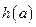 ;
;
(3)对(2)中的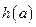 ,若关于
,若关于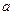 的方程
的方程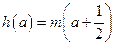 有两个不相等的实数解,求实数
有两个不相等的实数解,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数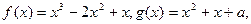 若函数
若函数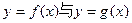 的图像有三个不同的交点,求实数a的取值范围。
的图像有三个不同的交点,求实数a的取值范围。
(本小题满分12分)
已知向量 ,
, ,函数
,函数 .
.
(1)求 的最大值及相应的
的最大值及相应的 的值;
的值;
(2)若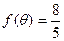 ,求
,求 的值.
的值.
(本小题满分12分)
某货轮在A处看灯塔B在货轮北偏东 ,距离为
,距离为 n mile;在A处看灯塔C在货轮的北偏西
n mile;在A处看灯塔C在货轮的北偏西 ,距离为
,距离为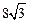 n mile.货轮由A处向正北航行到D处时,再看灯塔B在北偏东
n mile.货轮由A处向正北航行到D处时,再看灯塔B在北偏东 ,求:
,求:
(Ⅰ)A处与D处之间的距离;
(Ⅱ)灯塔C与D处之间的距离.