某校举行运动会,组委会招墓了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下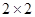 列联表:
列联表: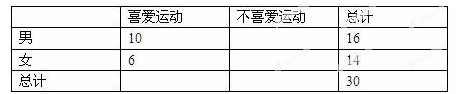
(2)根据列联表的独立性检验,有多大的把握认为性别与喜爱运动有关?
(3)从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人,求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率。
参考公式: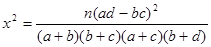 (其中
(其中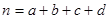 )
)
| |
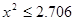 |
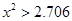 |
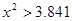 |
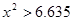 |
| 是否有关联 |
没有关联 |
90% |
95% |
99% |
(本小题满分13分)设数列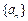 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:
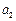
 ……
……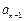
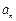 第1行
第1行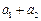
 ……
…… 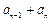 第2行
第2行
… … …
……
… 第 行
行
上表共有 行,其中第1行的
行,其中第1行的 个数为
个数为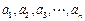 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
.
(1)求证:数列 成等比数列;
成等比数列;
(2)若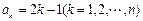 ,求和
,求和 .
.
(本小题满分13分)已 知
知 是函数
是函数 的极值点.
的极值点.
(1)当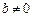 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)当 R时,函数
R时,函数
 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.
(本小题满分12分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.
(1)设 ,求y
,求y 关于
关于 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小 区的距离之和最小?
区的距离之和最小?
(本小题满分12分)在△ABC中,设角A,B,C的对边分别为a,b,c,若 ,
,
(1)求角A,B,C的大小;
(2)若BC边上的中线AM的长为 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分12分)已知A,B,C三点的坐标分别为 ,
, ,
, ,其中
,其中 .
.
(1)若 ,求角
,求角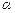 的值;
的值;
(2)若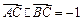 ,求
,求 的值.
的值.