高空遥感探测卫星在距地球表面高为h处绕地球转动,如果地球质量为M,地球半径为R,人造卫星质量为m,万有引力常量为G,求:
(1)人造卫星的角速度多大?
(2)人造卫星绕地球转动的周期是多少?
(3)人造卫星的向心加速度多大?
如图所示,垂直于纸面向里的匀强磁场有明显的圆形边界,圆心为O,半径为R,磁感应强度为B,现在在纸面内放上圆线圈,圆心在O处,半径为r(r<R),共有N匝。求:穿过这个线圈的磁通量。
如图所示,在正交坐标系Oxyz中,分布着电场和磁场(图中未画出).在Oyz平面的左方空间内存在沿y轴负方向、磁感应强度大小为B的匀强磁场;在Oyz平面右方、Oxz平面上方的空间内分布着沿z轴负方向、磁感应强度大小也为B匀强磁场;在Oyz平面右方、Oxz平面下方分布着沿y轴正方向的匀强电场.在t=0时刻,一质量为m、电荷量为+q的微粒从P点静止释放,已知P点的坐标为(5a,﹣2a,0),电场强度大小为 ,不计微粒的重力.求:
,不计微粒的重力.求: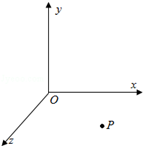
(1)微粒第一次到达x轴的速度大小v和时刻t1;
(2)微粒第一次到达y轴的坐标和时刻t2;
(3)假设在平面Oyz存在一层特殊物质,使微粒每次经过Oyz平面时,速度大小总变为原来的 ,求在时刻t3=t2+
,求在时刻t3=t2+ 时,电荷所在位置的坐标.
时,电荷所在位置的坐标.
在如图所示的电路中,R1=2Ω,R2=R3=4Ω,当电键K接a时,R2上消耗的电功率为4W,当电键K接b时,电压表示数为4.5V.试求: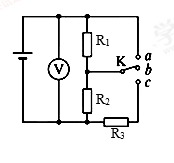
(1)当电键K接a时,通过电源的电流和电源两端的电压;
(2)电源的电动势和内电阻;
(3)当电键K接c时,求电源输出功率.
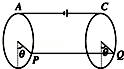
有两个相同的全长电阻为9Ω的均匀光滑圆环,固定于一个绝缘的水平台面上,两环分别在两个互相平行的、相距为20cm的竖直面内,两环的连心线恰好与环面垂直,两环面间有方向竖直向下的磁感应强度B=0.865T的匀强磁场,两环的最高点A和C间接有一内阻为0.5Ω的电源,连接导线的电阻不计.今有一根质量为10g,电阻为1.5Ω的棒置于两环内侧且可顺环滑动,而棒恰好静止于如图所示的水平位置,它与圆弧的两接触点P、Q和圆弧最低点间所夹的弧对应的圆心角均为θ=60°,取重力加速度g=10m/s2.试求此电源电动势E的大小.(取 )
)
质量为m、电荷量为q的带负电粒子由静止开始释放,经M、N板间的电场加速后,从A点垂直于磁场边界射入宽度为d的匀强磁场中,该粒子离开磁场时的位置P偏离入射方向的距离为L,如图所示。已知M、N两板间的电压为U,粒子的重力不计。求:匀强磁场的磁感应强度B。