已知函数 ,
, ,其中
,其中 是
是 的导函数.
的导函数.
(1)对满足 的一切
的一切 的值,都有
的值,都有 ,求实数
,求实数 的取值范围;
的取值范围;
(2)设 ,当实数
,当实数 在什么范围内变化时,函数
在什么范围内变化时,函数 的图象与直线
的图象与直线 只有一个公共点.
只有一个公共点.
在数列 中,
中, ,
,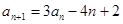 ,其中
,其中 .
.
(1)设 ,求数列
,求数列 的通项公式;
的通项公式;
(2)记数列 的前
的前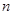 项和为
项和为 ,试比较
,试比较 与
与 的大小.
的大小.
2012年春晚歌舞类节目成为春晚顶梁柱,尤其是不少创意组合都被网友称赞很有新意.王力宏和李云迪的钢琴PK,加上背景板的黑白键盘,更被网友称赞是行云流水的感觉.某网站从2012年1月23号到1月30做了持续一周的在线调查,共有n人参加调查,现将数据整理分组如题中表格所示.
| 序号 |
年龄分组 |
组中值 |
频数(人数) |
频率(f) |
| 1 |
[20,25) |
22.5 |
x |
s |
| 2 |
[25,30) |
27.5 |
800 |
t |
| 3 |
[30,35) |
32.5 |
y |
0.40 |
| 4 |
[35,40) |
37.5 |
1600 |
0.32 |
| 5 |
[40,45) |
42.5 |
z |
0.04 |
(1)求n及表中x,y,z,s,t的值
(2)为了对数据进行分析,采用了计算机辅助计算,分析其中一部分计算,见算法流程图,求输出的S值,并说
明S的统计意义.
(3)从年龄在[20,30)岁人群中采用分层抽样法抽取6人参加元宵晚会活动,其中选取2人作为代表发言,求选取2名代表中恰有1人年龄在[25,30)岁的概率.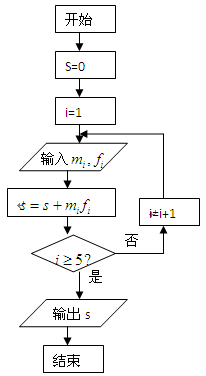
(本小题满分14分)
已知函数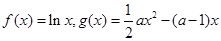 ,(
,(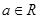 ).
).
(Ⅰ)已知函数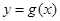 的零点至少有一个在原点右侧,求实数
的零点至少有一个在原点右侧,求实数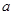 的范围.
的范围.
(Ⅱ)记函数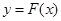 的图象为曲线
的图象为曲线 .设点
.设点 ,
,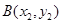 是曲线
是曲线 上的不同两点.如果在曲线
上的不同两点.如果在曲线 上存在点
上存在点 ,使得:①
,使得:① ;②曲线
;②曲线 在点
在点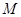 处的切线平行于直线
处的切线平行于直线 ,则称函数
,则称函数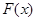 存在“中值相依切线”.
存在“中值相依切线”.
试问:函数 (
(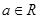 且
且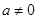 )是否存在“中值相依切线”,请说明理由.
)是否存在“中值相依切线”,请说明理由.
(本小题满分14分)
设集合W是满足下列两个条件的无穷数列{an}的集合:① , ②
, ②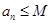 .其中
.其中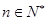 ,
, 是与
是与 无关的常数.
无关的常数.
(Ⅰ)若{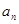 }是等差数列,
}是等差数列,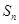 是其前
是其前 项的和,
项的和, ,
,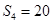 ,证明:
,证明: ;
;
(Ⅱ)设数列{ }的通项为
}的通项为 ,且
,且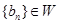 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设数列{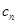 }的各项均为正整数,且
}的各项均为正整数,且 .证明
.证明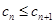 .
.
(本小题满分14分)
一动圆与圆 外切,与圆
外切,与圆 内切.
内切.
(I)求动圆圆心M的轨迹方程.(II)试探究圆心M的轨迹上是否存在点 ,使直线
,使直线 与
与 的斜率
的斜率 ?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).