在正项等比数列 中,
中, ,
,  .
.
(1) 求数列 的通项公式
的通项公式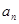 ;
;
(2) 记 ,求数列
,求数列 的前n项和
的前n项和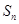 ;
;
(3) 记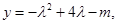 对于(2)中的
对于(2)中的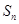 ,不等式
,不等式 对一切正整数n及任意实数
对一切正整数n及任意实数 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
.如图直角梯形OABC中,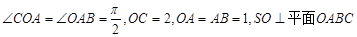 ,
,
SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
(Ⅰ)求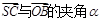 的余弦值;
的余弦值;
(Ⅱ)设
①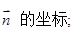
②设OA与平面SBC所成的角为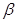 ,求
,求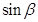 。
。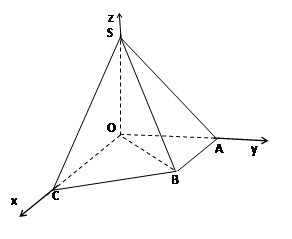
在数列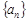 中,
中,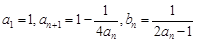 ,其中
,其中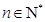 .
.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)求证: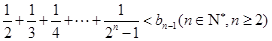
.已知点C(1,0),点A、B是⊙O: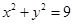 上任意两个不同的点,且满足
上任意两个不同的点,且满足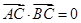 ,设P为弦AB的中点.(1)求点P的轨迹T的方程;(2)试探究在轨迹T上
,设P为弦AB的中点.(1)求点P的轨迹T的方程;(2)试探究在轨迹T上
是否存在这样的点:它到直线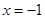 的距离恰好等于到点C的距离?若存在,求出这样的
的距离恰好等于到点C的距离?若存在,求出这样的
点的坐标;若不存在,说明理由.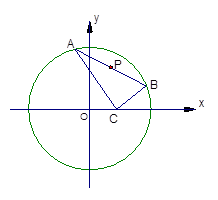
求证: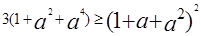 。
。
已知复数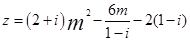 。当
。当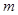 取什么值时,复数
取什么值时,复数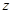 是
是
(1)0
(2)虚数;
(3)纯虚数;
(4)复平面内第二、四象限角平分线上的点对应的复数。