某班级共有60名学生,先用抽签法从中抽取部分学生调查他们的学习情况,若每位学生被抽到的概率为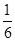 .
.
(1)求从中抽取的学生数;
(2)若抽查结果如下,先确定x,再完成频率分布直方图;
| 每周学习时间(小时) |
[0,10) |
[10,20) |
[20,30) |
[30,40] |
| 人数 |
2 |
4 |
x |
1 |
(3)估计该班学生每周学习时间的平均数(同一组中的数据用该组区间的中点值作代表).
在城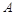 的西南方向上有一个观测站
的西南方向上有一个观测站 ,在城
,在城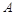 的南偏东
的南偏东 的方向上有一条笔直的公路,一辆汽车正沿着该公路上向城
的方向上有一条笔直的公路,一辆汽车正沿着该公路上向城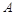 驶来.某一刻,在观测站
驶来.某一刻,在观测站 处观测到汽车与
处观测到汽车与 处相距
处相距 ,在
,在 分钟后观测到汽车与
分钟后观测到汽车与 处相距
处相距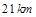 .若汽车速度为
.若汽车速度为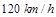 ,求该汽车还需多长时间才能到达城
,求该汽车还需多长时间才能到达城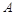 ?
?
已知函数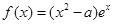 .
.
(I) 若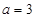 ,求
,求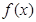 的单调区间;
的单调区间;
(II)已知 是
是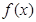 的两个不同的极值点,且
的两个不同的极值点,且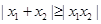 ,若
,若 恒成立,求实数b的取值范围.
恒成立,求实数b的取值范围.
已知动点 到点
到点 的距离,等于它到直线
的距离,等于它到直线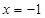 的距离.
的距离.
(Ⅰ)求点 的轨迹
的轨迹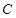 的方程;
的方程;
(Ⅱ)过点 任意作互相垂直的两条直线
任意作互相垂直的两条直线 ,分别交曲线
,分别交曲线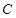 于点
于点 和
和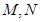 .设线段
.设线段 ,
,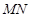 的中点分别为
的中点分别为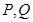 ,求证:直线
,求证:直线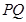 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求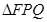 面积的最小值.
面积的最小值.
如图,在长方体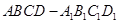 中,
中,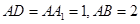 ,点
,点 在棱
在棱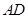 上移动
上移动
(Ⅰ)证明: ;
;
(Ⅱ)当 为
为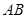 的中点时,求点
的中点时,求点 到面
到面 的距离;
的距离;
|
(Ⅲ)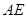 等于何值时,二面角
等于何值时,二面角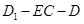 的大小为
的大小为