已知函数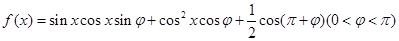 ,其图象过点
,其图象过点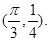
(1)求 的值;
的值;
(2)将函数 图象上各点向左平移
图象上各点向左平移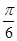 个单位长度,得到函数
个单位长度,得到函数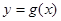 的图象,求函数
的图象,求函数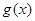 在
在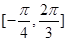 上的单调递增区间.
上的单调递增区间.
已知函数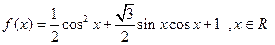 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在
在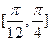 上的最大值和最小值,并求函数取得最大值和最小值时的自变量
上的最大值和最小值,并求函数取得最大值和最小值时的自变量 的值.
的值.
如图,在平面直角坐标系 中,以
中,以 轴为始边做两个锐角
轴为始边做两个锐角 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为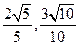
(1)求 的值; (2)求
的值; (2)求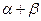 的值.
的值.
已知椭圆的中心为坐标原点O,焦点在x轴上,过椭圆右焦点F2且斜率为1的直线交椭圆于A、B两点,弦AB的中点为T,OT的斜率为 ,
,
(1)求椭圆的离心率;
(2)设Q是椭圆上任意一点,F1为左焦点,求 的取值范围;
的取值范围;
(3)若M、N是椭圆上关于原点对称的两个点,点P是椭圆上任意一点,当直线PN斜率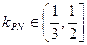 ,试求直线PM的斜率
,试求直线PM的斜率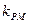 的范围。
的范围。
同时投掷两个骰子,计算下列事件的概率:
(1)事件A:两个骰子点数相同;
(2)事件B:两个骰子点数之和是4的倍数;
(3)事件C:两个骰子点数之差是2 。
下表是某小卖部5天卖出热茶的杯数与当天气温的对比表:
| 气温/℃ |
26 |
18 |
13 |
10 |
3 |
| 杯数 |
20 |
24 |
34 |
38 |
54 |
(1)请求出线性回归直线方程;
(2)如果某天的气温是-5℃时,预测这天小卖部卖出热茶的杯数。
(求线性回归方程系数公式 ,
,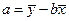 )
)