在等差数列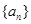
中，
.
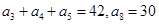（1）求数列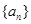的通项公式；
（2）若数列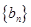
满足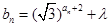
（
），则是否存在这样的实数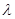
使得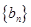为等比数列；
（3）数列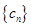
满足
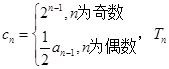为数列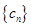的前n项和，求
.
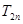（本题10分）
求证：△ABC是等边三角形的充要条件是a2＋b2＋c2＝ab＋ac＋bc。这里a、b、c是△ABC的三条边。
( 14分)
已知椭圆C的中心为直角坐标系x0y的原点，焦点在
轴上，它的一个项点到两个焦点的距离分别是7和1
(1)求椭圆C的方程
(2)若
为椭圆C的动点，M为过P且垂直于轴的直线上的点，
（e为椭圆C的离心率），求点M的轨迹方程，并说明轨迹是什么曲线。
已知椭圆中心在原点，焦点在
x轴上，长轴长等于12，离心率为
.
（Ⅰ）求椭圆的标准方程；
（Ⅱ
）过椭圆左顶点作直线l垂直于x轴
，若动点M到椭圆右焦点的距离比它到直线l的距离小4，求点M的轨迹方程.
过抛物线y2＝4x的焦点F作直线l，交抛物线于A、B两点，若线段AB的中点的横坐标为3，求|AB|
（1）求抛物线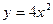
在点（1,4）处的切线方程
（2）求曲线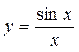
在点M(π，0)处的切线的斜率