已知函数f(x)=- x3+
x3+ x2-2x(a∈R).
x2-2x(a∈R).
(1)当a=3时,求函数f(x)的单调区间;
(2)若对于任意x∈[1,+∞)都有f′(x)<2(a-1)成立,求实数a的取值范围;
(3)若过点 可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
某公司生产一种硬纸片包装盒,如图,把正方形ABCD切去阴影部分所示的四个全等的等腰直角三角形,沿虚线折起使ABCD四个点重合,形成如图所示的正四棱柱包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AB=40cm, AE=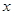 cm
cm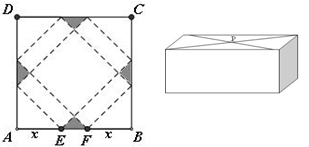
(1)要使包装盒侧面积S(cm )最大,则
)最大,则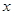 应取何值?
应取何值?
(2)要使包装盒容积V(cm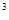 )最大,则
)最大,则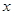 应取何值?并求出此时包装盒的高与底面边长的比值。
应取何值?并求出此时包装盒的高与底面边长的比值。
数列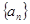 的前
的前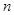 项和为
项和为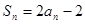 ,数列
,数列 是首项为
是首项为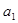 ,公差不为零的等差数列,且
,公差不为零的等差数列,且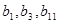 成等比数列.
成等比数列.
(1)求数列 与
与 的通项公式;
的通项公式;
(2)设数列 满足
满足 ,前n项和为
,前n项和为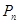 ,对于
,对于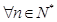 不等式
不等式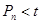 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
已知 为坐标原点,对于函数
为坐标原点,对于函数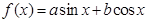 ,称向量
,称向量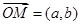 为函数
为函数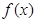 的伴随向量,设函数
的伴随向量,设函数 ,
,
(Ⅰ)求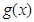 的伴随向量
的伴随向量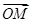 的模;
的模;
(Ⅱ)若 =
=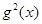 ,求
,求 在
在 内的最值及对应x的值.
内的最值及对应x的值.
已知函数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时有
时有 .
.
(1)判断函数 的单调性,并求使不等式
的单调性,并求使不等式 成立的实数
成立的实数 的取值范围.
的取值范围.
(2)若 、
、 、
、 分别是
分别是 的三个内角
的三个内角 、
、 、
、 所对的边,
所对的边, 面积
面积 求
求 、
、 的值;
的值;
设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若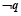 是
是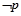 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.