我市南山区两村盛产荔枝,甲村有荔枝200吨,乙村有荔枝300吨.现将这些荔枝运到A,B两个冷藏仓库,已知A仓库可储存240吨,B仓库可储存260吨;从甲村运往A、B两处的费用分别为每吨20元和25元,从乙村运往A,B两处的费用分别为每吨15元和18元.设从甲村运往A仓库的荔枝重量为 吨,甲、乙两村运往两仓库的荔枝运输费用分别为
吨,甲、乙两村运往两仓库的荔枝运输费用分别为 元和
元和 元.
元.
(1)请填写下表,并求出 、
、 与
与 之间的函数关系式;
之间的函数关系式;
(2)试讨论甲、乙两村中,哪个村的运费较少;
(3)考虑到乙村的经济承受能力,乙村的荔枝运费不得超过4830元.在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值.
如图,抛物线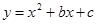 与x轴交于A(-1,0)和B(3,0)两点,交y轴于E.
与x轴交于A(-1,0)和B(3,0)两点,交y轴于E.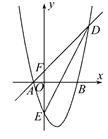
(1)求此抛物线的表达式.
(2)若直线y=x+1与抛物线交于A,D两点,与y轴交于点F,连接DE,求△DEF的面积.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°, ∠E=45°,∠A=60° ,AC=10,试求CD的长.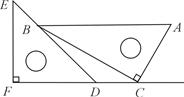
如图,已知平面直角坐标系中,⊙O的圆心在坐标原点,直线l与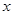 轴相交于点P,与⊙O相交于A、B两点,∠AOB=90°.点A和点B的横坐标是方程
轴相交于点P,与⊙O相交于A、B两点,∠AOB=90°.点A和点B的横坐标是方程 的两根,且两根之差为3.
的两根,且两根之差为3.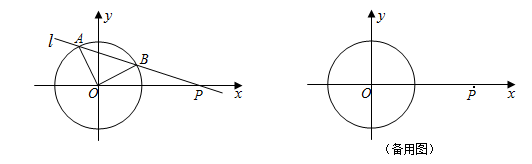
(1)求方程 的两根;
的两根;
(2)求A、B两点的坐标及⊙O的半径;
(3)把直线l绕点P旋转,使直线l与⊙O相切,求直线l的解析式.
如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1,∠BAE=30°.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB'E'(如图2),使点E落在CD边上的点E'处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
某衬衣店将进价为30元的一种衬衣以40元售出,平均每月能售出600件,调查表明:这种衬衣售价每上涨1元,其销售量将减少10件.
(1)写出月销售利润y(单位:元)与售价x(单位:元/件)之间的函数解析式.
(2)当销售价定为45元时,计算月销售量和销售利润.
(3)衬衣店想在月销售量不少于300件的情况下,使月销售利润达到10000元,销售价应定为多少?
(4)当销售价定为多少元时会获得最大利润?求出最大利润.