如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1,∠BAE=30°.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB'E'(如图2),使点E落在CD边上的点E'处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
在一个不透明的箱子里,装有红、白、黑各一个球,它们除了颜色之外没有其他区别.
(1)随机地从箱子里取出1个球,则取出红球的概率是多少?
(2)随机地从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示所有等可能的结果,并求两次取出相同颜色球的概率.
用适当的方法解下列方程
(1)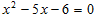
(2)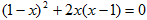
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A, B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大.
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一 边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号的汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得数据如下表:
(1)以车速为x轴,以刹车距离为y轴,建立平面直角坐标系,根据上表对应值作出函数的大致图象;
(2)观察图象估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5 m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?
如图,在菱形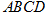 中,对角线
中,对角线 与
与 相交于点
相交于点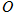 ,
, ,在菱形
,在菱形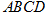 的外部以
的外部以 为边作等边三角形
为边作等边三角形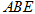 。点
。点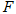 是对角线
是对角线 上一动点(点
上一动点(点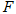 不与点
不与点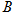 、D重合),将线段
、D重合),将线段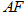 绕点
绕点 顺时针方向旋转
顺时针方向旋转 得到线段
得到线段 ,连接
,连接 。
。
(1)求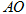 的长;
的长;
(2)如图2,当点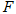 在线段
在线段 上,且点
上,且点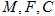 三点在同一条直线上时,求证:
三点在同一条直线上时,求证: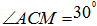
(3)连接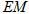 ,若
,若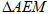 的面积为40,请画出图形,并直接写出
的面积为40,请画出图形,并直接写出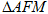 的周长。
的周长。