设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b1(a2-a1)=b2.
(1)求数列{an}和{bn}的通项公式;
(2)设cn= an bn,求数列{cn}的前n项和Tn.
an bn,求数列{cn}的前n项和Tn.
已知 ,
, ,且
,且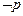 是
是
的必要不充分条件,求实数 的取值范围.
的取值范围.

(本小题满分14分)给出50个数,1,3,6,10,15,…,其规律是:第1个数是1,第2个数比第1个数大2,第3个数比第2个数大3,第4个数比第3个数大4,…,以此类推. 要求计算这50个数的和. 先将下面给出的程序框图补 充完整,再根据程序框图写出对应程序.
充完整,再根据程序框图写出对应程序.
1. 把程序框图补充完整:
(1)________________________ (3分)
(2)________________________ (4分)
2. 对应程序:
(本小题满分13分)在人群流量 较大的街道,有一中年
较大的街道,有一中年 人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3 个球为2个黄球1个白球的概率是多少?
个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
(本小题满分13分)为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图,根据统计图:
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?
(3)甲、乙两 个网站哪个更受欢迎?并说明理由。
个网站哪个更受欢迎?并说明理由。 