已知二次函数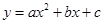 中,其函数
中,其函数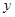 与自变量
与自变量 之间的部分对应值如下表所示:
之间的部分对应值如下表所示:
| x |
…… |
0 |
1 |
2 |
3 |
4 |
5 |
…… |
| y |
…… |
4 |
1 |
0 |
1 |
4 |
9 |
…… |
(1)当x=-1时,y的值为 ;
(2)点A(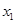 ,
, )、B(
)、B(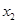 ,
,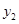 )在该函数的图象上,则当
)在该函数的图象上,则当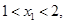
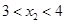 时,
时, 与
与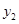 的大小关系是 ;
的大小关系是 ;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式: ;
(4)设点P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)都在二次函数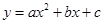 的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】
的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】
如图,在凯里市某广场上空飘着一只汽球P,A、B是地面上相距90米的两点,它们分别在汽球的正西和正东,测得仰角∠PAB=45°,仰角∠PBA=30°,求汽球P的高度.(精确到0.1米, =1.732)
=1.732)
小莉的爸爸有一张电影门票,她和哥哥两人都想去观看,可门票只有一张,读九年级的哥哥想了个办法,拿出八张扑克牌,将数字1,2,3,5的四张给妹妹,将数字4,6,7,8的四张留给自己,并按下列游戏规则进行:小莉和哥哥从各自的牌中随机抽出一张,然后两张牌的数字相加,如果和为偶数,则小莉去,如果和为奇数则哥哥去.
(1)用树状图或列表法求小莉能去看电影的概率.
(2)哥哥设计的游戏规则公平吗?请说明理由。
我校课题研究小组对本校九年级全体同学体育测试情况进行调查,他们随机抽查部分同学体育测试成绩(由高到低分 四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
请根据以上不完整的统计图提供的信息,
解答下列问题:
(1)该课题研究小组共抽查了____名同学的体育测试成绩,扇形统计图中的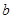 =___.
=___.
(2)补全条形统计图;
(3)若我校九年级共有300名同学,请估计我校九年级同学体育测试达标(测试成绩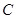 级
级
以上,含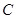 级)约有___________名.
级)约有___________名.
先化简,再选择一个你喜欢的娄(要合适哦!)代入求值: