过直线y=﹣1上的动点A(a,﹣1)作抛物线y=x2的两切线AP,AQ,P,Q为切点.
(1)若切线AP,AQ的斜率分别为k1,k2,求证:k1•k2为定值.
(2)求证:直线PQ过定点.
设锐角三角形ABC的内角A、B、C的对边分别为a、b、c,a=2bsinA.
(1)求B的大小;
(2)若a=3 ,c=5,求b.
,c=5,求b.
(1)若- <α<β<
<α<β< ,求α-β的取值范围.
,求α-β的取值范围.
(2)若x=(a+3)(a-5),y=(a+2)(a-4),比较x与y的大小.
如图, 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线内一定点,
为抛物线内一定点, 为抛物线上一动点,且
为抛物线上一动点,且 的最小值为
的最小值为 .
.
(1)求该抛物线的方程;
(2)如果过 的直线
的直线 交抛物线于
交抛物线于 、
、 两点,且
两点,且 ,求直线
,求直线 的倾斜角的取值范围.
的倾斜角的取值范围.
已知圆 ,定点N(1,0),
,定点N(1,0), 是圆
是圆 上任意一点,线段
上任意一点,线段 的垂直平分线
的垂直平分线 交
交 于点
于点 ,点
,点 的轨迹为曲线
的轨迹为曲线 。
。
(Ⅰ)求曲线 的方程;
的方程;
(2)若直线 与曲线
与曲线 相交于
相交于 ,
, 两点(
两点( 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
设椭圆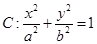
 的左、右焦点分别
的左、右焦点分别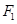 、
、 ,点
,点 是椭圆短轴的一个端点,且焦距为6,
是椭圆短轴的一个端点,且焦距为6,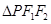 的周长为16.
的周长为16.
(Ⅰ)求椭圆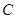 的方程;
的方程;
(Ⅱ)求过点 且斜率为
且斜率为 的直线
的直线 被椭圆
被椭圆 所截的线段的中点坐标.
所截的线段的中点坐标.