设椭圆 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,且椭圆的长轴长为
的离心率互为倒数,且椭圆的长轴长为 .
.
(Ⅰ)求椭圆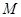 的方程;
的方程;
(Ⅱ)若直线 交椭圆
交椭圆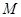 于
于 两点,
两点,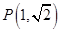 为椭圆
为椭圆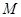 上一点,求
上一点,求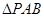 面积的最大值.
面积的最大值.
某渔业公司今年初用98万元购进一艘渔船用于捕捞,第一年需各种费用12万元,从第二年开始包括维修费在内,每年所需费用均比上一年增加4万元,该船每年捕捞的总收入为50万元.
(1)该船捕捞几年开始盈利?(即总收入减去成本及所有费用之差为正值)
(2)该船捕捞若干年后,处理方案有两种:
①当年平均盈利达到最大值时,以26万元的价格卖出;
②当盈利总额达到最大值时,以8万元的价格卖出.问哪一种方案较为合算,请说明理由.
某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 |
A |
B |
C |
D |
E E |
| 销售额(x)/千万元 |
3 |
5 |
6 |
7 |
9 9 |
| 利润额(y)/百万元 |
2 |
3 |
3 |
4 |
5 |
(1)画出销售额和利润额的散点图.
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程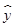 =bx+a,其中
=bx+a,其中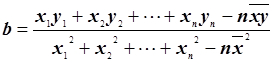
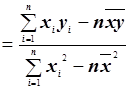 ,a=
,a=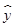 -b
-b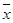 ;
;
(3)对计算结果进行简要的分析说明.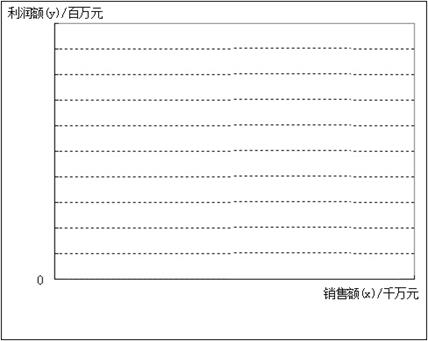
一农民有基本土地2亩,根据往年经验,若种玉米,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤.但玉米成本较高,每季每亩240元,而花生只需80元,且花生每公斤卖5元,玉米每公斤卖3元.现该农民手头有400元,两种作物各种多少,才能获得最大收益?
为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 |
频数 |
频率 |
| 145.5~149.5 |
1 |
0.02 |
| 149.5~153.5 |
4 |
0.08 |
| 153.5~157.5 |
20 |
0.40 |
| 157.5~161.5 |
15 |
0.30 |
| 161.5~165.5 |
8 |
0.16 |
| 165.5~169.5 |
m |
n |
| 合 计 |
M |
N |
(1)求出表中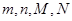 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?由直方图确定此组数据中位数是多少?
解下列不等式:
(1)-x2+2x- >0;
>0;
(2)解关于x的不等式