两枚质量均匀的正方体骰子,六个面上分别标有数字1、2、3、4、5、6,抛掷两枚骰子.记两枚骰子朝上的面上的数字分别为p,q,若把p,q分别作为点A的横坐标和纵坐标,
(1)用列表法或树状图表示出点A(p,q)所有可能出现的结果;
(2)求点A(p,q)在函数y=x-1的图象上的概率.
如图,已知正三棱柱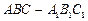 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是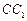 的中点,直线
的中点,直线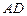 与侧面
与侧面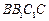 所成的角是
所成的角是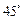 .
.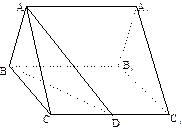
⑴求二面角 的大小;
的大小;
⑵求点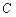 到平面
到平面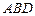 的距离.
的距离.
2010年上海世博会大力倡导绿色出行,并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放量.某游客计划在游园期间种植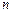 棵树,已知每棵树是否成活互不影响,成活率都为
棵树,已知每棵树是否成活互不影响,成活率都为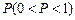 ,用
,用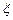 表示他所种植的树中成活的棵数,
表示他所种植的树中成活的棵数,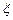 的数学期望为
的数学期望为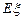 ,方差为
,方差为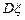 .
.
⑴若 ,求
,求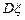 的最大值;
的最大值;
⑵已知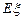
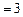 ,标准差
,标准差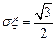 ,试求
,试求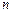 与
与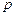 的值并写出
的值并写出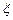 的分布列.
的分布列.
已知函数

 (
( ),且函数
),且函数 的最小正周期为
的最小正周期为 .
.
⑴求函数 的解析式;
的解析式;
⑵在△ 中,角
中,角 所对的边分别为
所对的边分别为 若
若 ,
, ,且
,且 ,试求
,试求 的值.
的值.
已知函数 .
.
(Ⅰ)求函数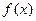 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(Ⅱ)求函数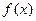 在区间
在区间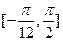 上的值域.
上的值域.
求值 (Ⅰ)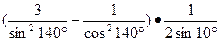 .
.
(Ⅱ)