某市直小学为了加强管理，对全校教职工实行新的临时事假制度：“每位教职工每月在正常的工作时间，临时有事，可请假至多三次，每次至多一小时”.现对该制度实施以来50名教职工请假的次数进行调查统计，结果如下表所示：
| 请假次数 |
 |
 |
 |
 |
| 人数 |
 |
 |
 |
 |
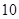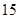根据上表信息解答以下问题：
(1)从该小学任选两名教职工，用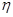
表示这两人请假次数之和，记“函数
在区间
上有且只有一个零点”为事件
，求事件发生的概率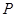
；
(2)从该小学任选两名职工，用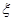
表示这两人请假次数之差的绝对值，求随机变量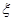的分布列及数学期望
.
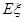已知抛物线y=x2－1上一定点B(－1，0)和两个动点P、Q，当P在抛物线上运动时，BP⊥PQ，则Q点的横坐标的取值范围是_________
条件：(1)截
轴弦长为2.(2)被
轴分成两段圆弧，其弧长之比为3:1在满足(1)(2)的所有圆中，求圆心到直线
距离最小时圆的方程.
画出以A（3，－1）、B（－1，1）、C（1，3）为顶点的△ABC的区域（包括各边），写出该区域所表示的二元一次不等式组，并求以该区域为可行域的目标函数z=3x－2y的最大值和最小值
直线l的方程为y=x+3,在l上任取一点P，若过点P且以双曲线12x2－4y2=3的焦点作椭圆的焦点，那么具有最短长轴的椭圆方程为_________
点A、B分别是椭圆
长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于
轴上方，
.
（1）求点P的坐标；
（2）设M是椭圆长轴AB上的一点，M到直线AP的距离等于
，求椭圆上的点到点M的距离
的最小值.