从某学校的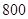 名男生中随机抽取
名男生中随机抽取 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于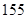 cm和
cm和 cm之间,将测量结果按如下方式分成八组:第一组[
cm之间,将测量结果按如下方式分成八组:第一组[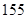 ,
,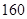 ),第二组[
),第二组[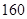 ,
,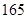 ),…,第八组[
),…,第八组[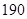 ,
, ],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为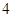 人.
人.
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的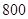 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在 cm以上(含
cm以上(含 cm)的人数;
cm)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为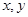 ,事件
,事件 {
{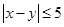 },事件
},事件 {
{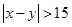 },求
},求 .
.
设函数 ,
,
(1)求 的最小值
的最小值 ;
;
(2)当 时,求
时,求 的最小值.
的最小值.
在平面直角坐标系 中,以
中,以 为极点,
为极点, 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数),两曲线相交于
为参数),两曲线相交于 两点.
两点.
(1)写出曲线 的直角坐标方程和直线
的直角坐标方程和直线 的普通方程;
的普通方程;
(2)若 求
求 的值.
的值.
已知矩阵
 ,若矩阵
,若矩阵 属于特征值6的一个特征向量为
属于特征值6的一个特征向量为 ,属于特征值1的一个特征向量
,属于特征值1的一个特征向量 .
.
(1)求矩阵 的逆矩阵;
的逆矩阵;
(2)计算
已知动圆 过定点(1,0),且与直线
过定点(1,0),且与直线 相切.
相切.
(1)求动圆圆心 的轨迹方程;
的轨迹方程;
(2)设 是轨迹
是轨迹 上异于原点
上异于原点 的两个不同点,直线
的两个不同点,直线 和
和 的倾斜角分别为
的倾斜角分别为 和
和 ,①当
,①当 时,求证直线
时,求证直线 恒过一定点
恒过一定点 ;
;
②若 为定值
为定值 ,直线
,直线 是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
是否仍恒过一定点,若存在,试求出定点的坐标;若不存在,请说明理由.
如图,直角梯形 中,
中, ,点
,点 分别是
分别是 的中点,点
的中点,点 在
在 上,沿
上,沿 将梯形
将梯形 翻折,使平面
翻折,使平面
 平面
平面 .
.
(1)当 最小时,求证:
最小时,求证: ;
;
(2)当 时,求二面角
时,求二面角 平面角的余弦值.
平面角的余弦值.