已知抛物线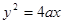 (
(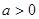 且
且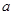 为常数),
为常数),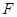 为其焦点.
为其焦点.
(1)写出焦点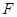 的坐标;
的坐标;
(2)过点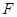 的直线与抛物线相交于
的直线与抛物线相交于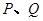 两点,且
两点,且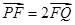 ,求直线
,求直线 的斜率;
的斜率;
(3)若线段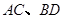 是过抛物线焦点
是过抛物线焦点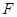 的两条动弦,且满足
的两条动弦,且满足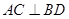 ,如图所示.求四边形
,如图所示.求四边形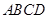 面积的最小值
面积的最小值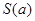 .
.
如图,在四棱锥P-ABCD中,侧面PAD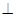 底面ABCD,侧棱
底面ABCD,侧棱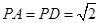 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB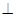 AD,AD=2,AB=BC=l,E为AD中点.
AD,AD=2,AB=BC=l,E为AD中点.
(1)求证:PE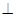 平面ABCD:
平面ABCD:
(2)求异面直线PB与CD所成角的余弦值:
(3)求平面PAB与平面PCD所成的二面角.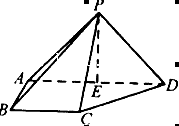
某超市在节日期间进行有奖促销,凡在该超市购物满200元的顾客,将获得一次摸奖机会,规则如下:
奖盒中放有除颜色外完全相同的1个红色球,1个黄色球,1个蓝色球和1个黑色球.顾客不放回的每次摸出1个球,直至摸到黑色球停止摸奖.规定摸到红色球奖励10元,摸到黄色球或蓝色球奖励5元,摸到黑色球无奖励.
(1)求一名顾客摸球3次停止摸奖的概率;
(2)记X为一名顾客摸奖获得的奖金数额,求随机变量X的分布列和数学期望.
己知A、B、C分别为△ABC的三边a、b、c所对的角,向量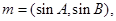
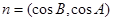 ,且
,且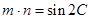 .
.
(1)求角C的大小:
(2)若sinA,sinC,sinB成等差数列,且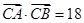 ,求边c的长.
,求边c的长.
已知函数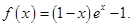
(1)求函数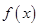 的最大值;
的最大值;
(2)若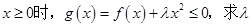 的取值范围.
的取值范围.
设椭圆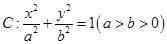 的左、右焦点分别为
的左、右焦点分别为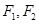 ,上顶点为A,在x轴负半轴上有一点B,满足
,上顶点为A,在x轴负半轴上有一点B,满足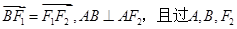 三点的圆与直线
三点的圆与直线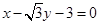 相切.
相切.
(1)求椭圆C的方程;
(2)过右焦点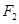 作斜率为k的直线
作斜率为k的直线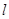 与椭圆C交于M,N两点,线段MN的垂直平分线与x轴相交于点P(m,0),求实数m的取值范围.
与椭圆C交于M,N两点,线段MN的垂直平分线与x轴相交于点P(m,0),求实数m的取值范围.