已知圆 ,经过椭圆
,经过椭圆 的右焦点
的右焦点 及上顶点
及上顶点 ,过圆外一点
,过圆外一点 倾斜角为
倾斜角为 的直线
的直线 交椭圆于
交椭圆于 两点.
两点.
(1)求椭圆的方程;
(2)若右焦点 在以线段CD为直径的圆
在以线段CD为直径的圆 的内部,求
的内部,求 的取值范围.
的取值范围.
如图,在棱长为1的正方体 中.
中.
(1)求异面直线 与
与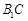 所成的角;
所成的角;
(2)求证平面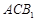 ⊥平面
⊥平面 .
.
阅读程序框图,回答以下问题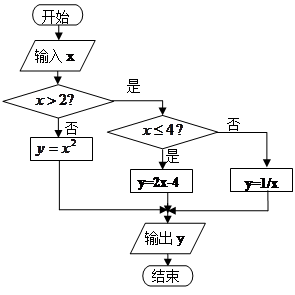
(1)该程序框图表达的函数解析式是什么?
(2)若要使输入的x值与输出的y值相等,则这样的x有几个,并分别写出来。
已知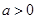 ,函数
,函数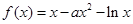 .
.
(1)若 是单调函数,求实数
是单调函数,求实数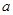 的取值范围;
的取值范围;
(2)若 有两个极值点
有两个极值点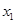 、
、 ,证明:
,证明: .
.
双曲线 与椭圆
与椭圆 有相同的焦点
有相同的焦点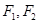 ,且该双曲线
,且该双曲线
的渐近线方程为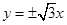 .
.
(1)求双曲线的标准方程;
(2) 过该双曲线的右焦点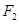 作斜率不为零的直线与此双曲线的左,右两支分别交于点
作斜率不为零的直线与此双曲线的左,右两支分别交于点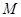 、
、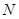 ,
,
设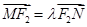 ,当
,当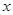 轴上的点
轴上的点 满足
满足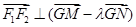 时,求点
时,求点 的坐标.
的坐标.
设等差数列 的前n项的和为
的前n项的和为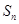 ,且
,且 .
.
(1)求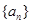 的通项公式;
的通项公式;
(2)令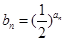 ,求
,求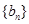 的前
的前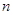 项和
项和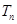 ;
;
(3)若不等式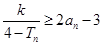 对于
对于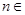 N
N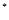 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.