已知椭圆的一个顶点为 ,焦点在
,焦点在 轴上,中心在原点.若右焦点到直线
轴上,中心在原点.若右焦点到直线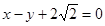 的距离为3.
的距离为3.
(1)求椭圆的标准方程;
(2)设直线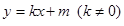 与椭圆相交于不同的两点
与椭圆相交于不同的两点 .当
.当 时,求
时,求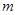 的取值范围.
的取值范围.
平面直角坐标系
中,过椭圆
右焦点的直线
交
于
两点,
为
的中点,且
的斜率为 .
.
(Ι)求
的方程;
(Ⅱ)
为
上的两点,若四边形
的对角线
,求四边形面积的最大值
经销商经销某种农产品,在一个销售季度内,每售出
该产品获利润
元,未售出的产品,每
亏损
元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示.经销商为下一个销售季度购进了
该农产品.以
(单位:
,
)表示下一个销售季度内经销该农产品的数量,
表示利润.

(Ⅰ)将
表示为
的函数
(Ⅱ)根据直方图估计利润
不少于
元的概率;
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若
,则取
,且
的概率等于需求量落入
,求
的数学期望.
如图,直棱柱
中,
分别是
的中点,
.

(Ⅰ)证明:
平面
;
(Ⅱ)求二面角
的正弦值.
在内角
的对边分别为
,已知
.
(Ⅰ)求
;
(Ⅱ)若
,求
面积的最大值.
已知双曲线
的左、右焦点分别为
离心率为 直线
与
的两个交点间的距离为
直线
与
的两个交点间的距离为
(I)求
;
(II)设过
的直线
与
的左、右两支分别相交有
两点,且
证明:
成等比数列