已知函数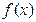 为
为 上的奇函数,且
上的奇函数,且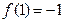 ,对任意
,对任意 ,有
,有 。(1)判断函
。(1)判断函 数
数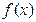 在
在 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(2)解关于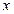 的不等式
的不等式
如图一,平面四边形 关于直线
关于直线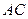 对称,
对称,
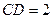 .
.
把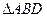 沿
沿 折起(如图二),使二面角
折起(如图二),使二面角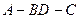 的余弦值等于
的余弦值等于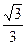 .对于图二,
.对于图二,
(Ⅰ)求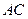 ;
;
(Ⅱ)证明: 平面
平面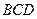 ;
;
(Ⅲ)求直线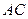 与平面
与平面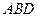 所成角的正弦值.
所成角的正弦值.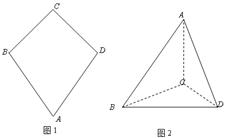
最近,李师傅一家 三口就如何将手中的10万块钱投资理财,提出了二种方案:第一种方案:将10万块钱全部用来买股,据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利的概率为
三口就如何将手中的10万块钱投资理财,提出了二种方案:第一种方案:将10万块钱全部用来买股,据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利的概率为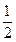 .第二种方案:将10万年钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可以损失10%,也可以不赔不赚,且三种情况发生的概率分别为
.第二种方案:将10万年钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可以损失10%,也可以不赔不赚,且三种情况发生的概率分别为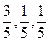 .
.
针对以上两种投资方案,请你为李师傅家选择一种合理的理财方法,并说明理由.
已知向量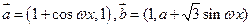 (
(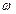 为常数且
为常数且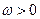 ),函数
),函数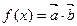 在
在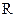 上的最大值为
上的最大值为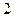 .(Ⅰ)求实数
.(Ⅰ)求实数 的值;(Ⅱ)把函数
的值;(Ⅱ)把函数 的图象向右平移
的图象向右平移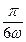 个单位,可得函数
个单位,可得函数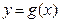 的图象,若
的图象,若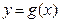 在
在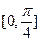 上为增函数,求
上为增函数,求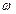 的最大值.
的最大值.
设数列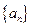 的前
的前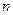 项和为
项和为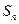 ,点
,点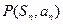 在直线
在直线 上,
上, 为常数,
为常数,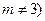 .
.
(Ⅰ)求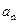 ;
;
(Ⅱ)若数列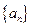 的公比
的公比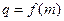 ,数列
,数列 满足
满足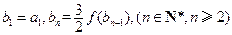 ,求证:
,求证: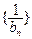 为等差数列,并求
为等差数列,并求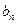 ;
;
(III)设数列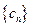 满足
满足 ,
, 为数列
为数列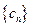 的前
的前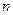 项和,且存在实数
项和,且存在实数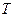 满足
满足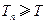 ,
,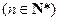 ,求
,求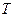 的最大值.
的最大值.