如图,在四棱柱 中, 平面 , , .
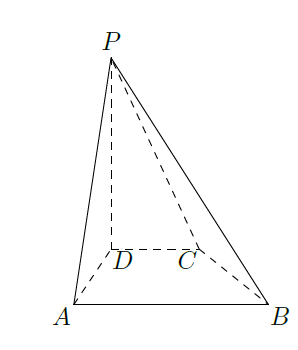
(1)当正视方向与向量
的方向相同时,画出四棱锥
的正视图(要求标出尺寸,并写出演算过程);
(2)若
为
的中点,求证:求二面角
.
(3)求三棱锥 的体积.
已知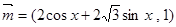 ,
, ,且
,且 .
.
(1)将 表示为
表示为 的函数
的函数 ,并求
,并求 的单调增区间;
的单调增区间;
(2)已知 分别为
分别为 的三个内角
的三个内角 对应的边长,若
对应的边长,若 ,且
,且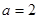 ,
,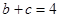 ,求
,求 的面积.
的面积.
已知定义在R上的函数f(x)= 的周期为
的周期为 ,
,
且对一切x R,都有f(x)
R,都有f(x) ;
;
(1)求函数f(x)的表达式;
(2)若g(x)=f( ),求函数g(x)的单调增区间.
),求函数g(x)的单调增区间.
已知函数 在一个周期内的图象下图所示。
在一个周期内的图象下图所示。
(1)求函数的解析式;
(2)设 ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。
已知函数 .
.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最大最小值及相应的x的值;
(3)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
已知函数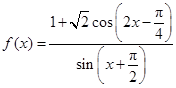 .
.
(Ⅰ)求 的定义域;
的定义域;
(Ⅱ)若角 在第一象限且
在第一象限且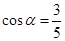 ,求
,求 .
.