某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为
,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得3分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。
(Ⅰ)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为
,求
的概率;
(Ⅱ)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
已知椭圆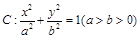 ,
,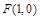 为其右焦点,离心率为
为其右焦点,离心率为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点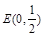 ,问是否存在直线
,问是否存在直线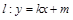 ,使
,使 与椭圆
与椭圆 交于
交于 两点,且
两点,且 .若存在,求出
.若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知等差数列 和公比为
和公比为
 的等比数列
的等比数列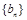 满足:
满足: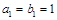 ,
,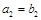 ,
, .
.
(Ⅰ)求数列 ,
,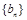 的通项公式;
的通项公式;
(Ⅱ)若数列 的前
的前 项和为
项和为 ,且对任意
,且对任意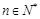 均有
均有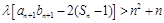 成立,试求实数
成立,试求实数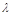 的取值范围.
的取值范围.
如图,已知四边形 为梯形,
为梯形, ,
, ,四边形
,四边形 为矩形,且平面
为矩形,且平面 平面
平面 ,
, ,点
,点 为
为 的中点.
的中点.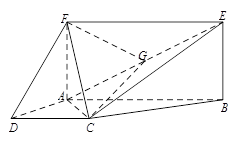
(Ⅰ)求证: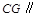 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求三棱锥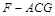 的体积.
的体积.
已知函数 (
( 为常数),且
为常数),且 在点
在点 处的切线平行于
处的切线平行于 轴.
轴.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求函数 的单调区间.
的单调区间.
2013年1月份,我国北方部分城市出现雾霾天气,形成雾霾天气主要原因与 有关.
有关.  是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.  日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:
日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:
 日均值k(微克) 日均值k(微克) |
空气质量等级 |
 |
一级 |
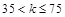 |
二级 |
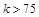 |
超标 |

某环保部门为了了解甲、乙两市的空气质量状况,在过去某月的30天中分别随机抽取了甲、乙两市6天的 日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市
日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市 日均值的样本平均数,并由此判断哪个市的空气质量较好;
日均值的样本平均数,并由此判断哪个市的空气质量较好;
(Ⅱ)若从甲市这6天的样本数据中随机抽取两天的数据,求恰有一天空气质量超标的概率.