如图,在三棱柱
中,
是边长为4的正方形.平面
平面
,
.

(Ⅰ)求证:
平面
;
(Ⅱ)求二面角
的余弦值;
(Ⅲ)证明:在线段
存在点
,使得
,并求
的值.
(本小题满分12分)某电视台有一档综艺节目,其中有一个抢答环节,有甲、乙两位选手进行抢答,规则如下:若选手抢到答题权,答对得20分,答错或不答则送给对手10分.已知甲每次抢到答题权的概率为 ,且答对的概率为
,且答对的概率为 ,乙抢到答题权的概率为
,乙抢到答题权的概率为 ,且答对的概率为
,且答对的概率为 .
.
(1)在一轮抢答中,甲得到0分的概率;
(2)若比赛进行两轮,求甲得分的分布列及其期望.
(本小题满分12分)已知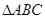 的三个内角A、B、C的对边分别为
的三个内角A、B、C的对边分别为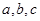 ,且
,且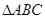 的面积
的面积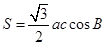 .
.
(1)求角B的大小;
(2)若 ,且
,且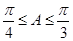 ,求边
,求边 的取值范围.
的取值范围.
(本小题满分13分)已知函数 ,其中
,其中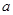 为常数,且
为常数,且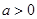 .
.
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线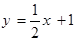 垂直,求
垂直,求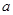 的值;
的值;
(2)若函数 在区间
在区间 上的最小值为
上的最小值为 ,求
,求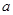 的值.
的值.
(本小题满分13分)如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是 ,双曲线的左、右顶点
,双曲线的左、右顶点 、
、 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.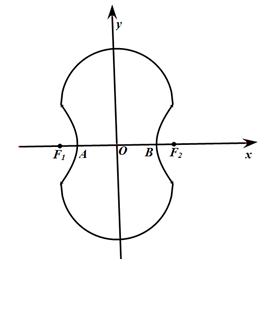
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为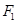 、
、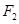 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点 ,使得
,使得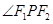 是直角.
是直角.
(本小题满分13分)设函数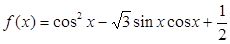
(Ⅰ)求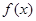 的最小正周期及值域;
的最小正周期及值域;
(Ⅱ)已知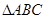 中,角
中,角 的对边分别为
的对边分别为 ,若
,若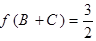 ,
, ,
,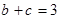 ,求
,求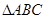 的面积.
的面积.