已知抛物线
的顶点为原点,其焦点
到直线
的距离为
.设
为直线
上的点,过点
作抛物线
的两条切线
,其中
为切点.
(1) 求抛物线
的方程;
(2) 当点
为直线
上的定点时,求直线
的方程;
(3) 当点
在直线
上移动时,求
的最小值.
已知曲线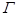 上任意一点
上任意一点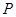 到两个定点
到两个定点 和
和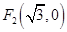 的距离之和为4.
的距离之和为4.
(1)求曲线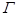 的方程;
的方程;
(2)设过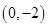 的直线
的直线 与曲线
与曲线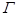 交于
交于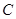 、
、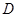 两点,且
两点,且 (
( 为坐标原点),求直线
为坐标原点),求直线 的方程.
的方程.
如图, 垂直于矩形
垂直于矩形 所在的平面,
所在的平面, 分别是
分别是 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 .
.
向量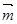 =(a+1,sinx),
=(a+1,sinx),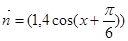 ,设函数g(x)=
,设函数g(x)=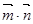 (a∈R,且a为常数).
(a∈R,且a为常数).
(1)若a为任意实数,求g(x)的最小正周期;
(2)若g(x)在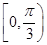 ,上的最大值与最小值之和为7,求a的值.
,上的最大值与最小值之和为7,求a的值.
已知函数f(x)= x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
(1)求a,b的值;
(2)求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(Ⅰ)A类工人中和B类工人各抽查多少工人?
(Ⅱ)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
| 生产能力分组 |
 |
 |
 |
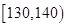 |
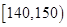 |
| 人数 |
4 |
8 |
 |
5 |
3 |
表2:
| 生产能力分组 |
 |
 |
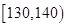 |
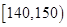 |
| 人数 |
6 |
y |
36 |
18 |
(i)、先确定 ,再完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
,再完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)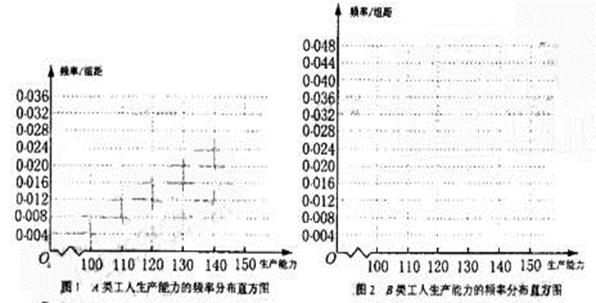 (ii)分别估计
(ii)分别估计 类工人和
类工人和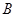 类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。