已知二次函数f(x)满足条件f(0)=1和f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在区间[-1,1]上的最大值和最小值.
.已知定义在R上的二次函数 满足
满足 ,且
,且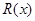 的最小值为0,函数
的最小值为0,函数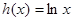 ,又函数
,又函数 。
。
(I)求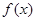 的单调区间;(II)当
的单调区间;(II)当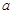 ≤
≤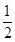 时,若
时,若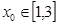 ,求
,求 的最小值;
的最小值;
(III)若二次函数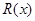 图象过(4,2)点,对于给定的函数
图象过(4,2)点,对于给定的函数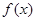 图象上的点A(
图象上的点A( ),
),
当 时,探求函数
时,探求函数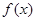 图象上是否存在点
图象上是否存在点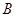 (
( )(
)(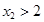 ),使
),使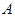 、
、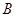 连线平行于
连线平行于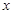 轴,并说明理由。(参考数据:e=2.71828…)
轴,并说明理由。(参考数据:e=2.71828…)
设椭圆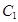 :
: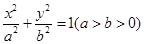 的左、右焦点分别是
的左、右焦点分别是 ,下顶点为
,下顶点为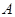 ,线段
,线段 的中点为
的中点为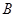 (
( 为坐标原点),如图.若抛物线
为坐标原点),如图.若抛物线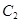 :
: 与
与 轴的交点为
轴的交点为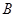 ,且经过
,且经过 点.
点.
(Ⅰ)求椭圆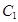 的方程;
的方程;
(Ⅱ)设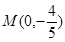 ,
,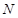 为抛物线
为抛物线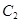 上的一动点,过点
上的一动点,过点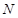 作抛物线
作抛物线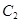 的切线交椭圆
的切线交椭圆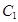 于
于 两点,求
两点,求 的最大值.
的最大值.
为进一步保障和改善民生,国家“十二五”规划纲要提出,“十二五”期间将提高住房
保障水平,使城镇保障性信房覆盖率达到20℅左右. 某城市2010年有商品房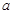 万套,保障
万套,保障
性住房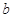 万套(
万套(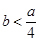 ). 预计2011年新增商品房
). 预计2011年新增商品房 万套,以后每年商品新增量是上一年新增
万套,以后每年商品新增量是上一年新增
量的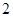 倍,问“十二五”期间(2011年~2015年)该城市保障性住房建设年均应增加多少
倍,问“十二五”期间(2011年~2015年)该城市保障性住房建设年均应增加多少
万套才能使覆盖率达到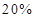 ?
?
( ,
,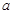 ,
,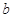 ,
, )
)
已知函数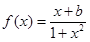 为奇函数。
为奇函数。
(I)证明:函数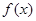 在区间(1,
在区间(1,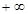 )上是减函数;
)上是减函数;
(II)解关于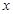 的不等式
的不等式 。
。
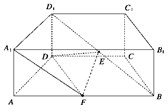
直四棱柱 中,底面
中,底面 是等腰梯形,
是等腰梯形,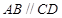 ,
,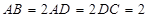 ,
,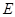 为
为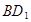 的中点,
的中点, 为
为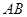 中点.
中点.
(1) 求证: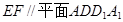 ;
;
(2) 若 ,求
,求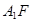 与平面
与平面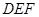 所成角的正弦值.
所成角的正弦值.