如图,四棱锥
中,
,
和
都是等边三角形.
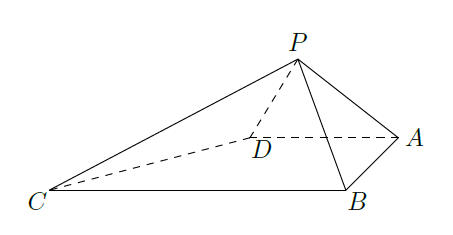
(Ⅰ)证明:
;
(Ⅱ)求二面角
的大小.
已知圆方程为 
(1)求圆心轨迹的参数方程 和普通方程;
和普通方程;
(2)点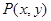 是(1)中曲线
是(1)中曲线 上的动点,求
上的动点,求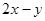 的取值范围.
的取值范围.
已知复数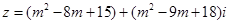 在复平面内表示的点为A,实数m取什么值时,
在复平面内表示的点为A,实数m取什么值时,
(1)复数z为实数?
(2)复数z为纯虚数?
(3)点A位于复平面的第三象限?
已知二次函数 满足条件:
满足条件:
① ;②
;② 的最小值为
的最小值为 。
。
(1)求函数 的解析式;
的解析式;
(2)设数列 的前
的前 项积为
项积为 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在(2)的条件下,若 是
是 与
与 的等差中项,试问数列
的等差中项,试问数列 中第几项的值最小?求出这个最小值。
中第几项的值最小?求出这个最小值。
如图,有两条相交成 角的直路
角的直路 ,交点为
,交点为 ,甲、乙分别在
,甲、乙分别在 上,起初甲离
上,起初甲离 点
点 ,乙离
,乙离 点
点 ,后来甲沿
,后来甲沿 的方向,乙沿
的方向,乙沿 的方向,同时以
的方向,同时以 的速度步行。
的速度步行。
(1)起初两人的距离是多少?
(2) 小时后两人的距离是多少?
小时后两人的距离是多少?
(3)什么时候两人的距离最短,并求出最短距离。
已知数列 的前
的前 项和
项和 ,设数列
,设数列 满足
满足 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设 ,求
,求 .
.