已知动点 , 都在曲线C: ( 为参数)上,对应参数分别为 与 ( ), 为 的中点。
(Ⅰ)求
的轨迹的参数方程
(Ⅱ)将
到坐标原点的距离
表示为
的函数,并判断
的轨迹是否过坐标原点。
已知抛物线C:y2=2px(p>0)过点A(1,-2).
(Ⅰ)求抛物线C的方程,并求其准线方程;
(Ⅱ)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于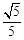 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
已知平面区域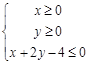 被圆C及其内部所覆盖.
被圆C及其内部所覆盖.
(Ⅰ)当圆C的面积最小时,求圆C的方程;
(Ⅱ)若斜率为1的直线l与(1)中的圆C交于不同的两点A、B,且满足CA⊥CB,求直线l的方程.
已知两条直线l1:ax-by+4=0,l2:(a-1)x+y+b=0,直线l1过点 ,并且直线l1与直线l2垂直.求满足条件的a,b的值.
,并且直线l1与直线l2垂直.求满足条件的a,b的值.
(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分.)
已知数列{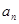 }满足:
}满足: ,
, 为数列
为数列 的前
的前 项和。
项和。
(1)若{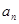 }是递增数列,且
}是递增数列,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)若 ,且{
,且{ }是递增数列,{
}是递增数列,{ }是递减数列,求数列{
}是递减数列,求数列{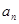 }的通项公式;
}的通项公式;
(3)若 ,对于给定的正整数
,对于给定的正整数 ,是否存在一个满足条件的数列
,是否存在一个满足条件的数列 ,使得
,使得 ,如果存在,给出一个满足条件的数列,如果不存在,请说明理由。
,如果存在,给出一个满足条件的数列,如果不存在,请说明理由。
(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分.)
已知椭圆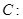
 的左、右焦点分别为
的左、右焦点分别为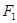 ,
,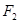 ,点
,点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形.
(1)求椭圆 的方程;
的方程;
(2)设点 是椭圆
是椭圆 上一动点,求线段
上一动点,求线段 的中点
的中点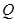 的轨迹方程;
的轨迹方程;
(3)过点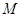 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
,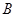 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,
,
且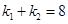 ,探究:直线
,探究:直线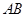 是否过定点,并说明理由.
是否过定点,并说明理由.