已知函数
.
(Ⅰ) 若直线
与
的反函数的图像相切, 求实数
的值;
(Ⅱ) 设
, 讨论曲线
与曲线
公共点的个数.
(Ⅲ) 设
, 比较
与
的大小, 并说明理由.
已知函数 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,
, ,求
,求 .
.
选修4-5:不等式选讲
已知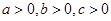 ,函数
,函数 的最小值为4.
的最小值为4.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的最小值.
的最小值.
选修4—4:坐标与参数方程
在直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.已知点A的极坐标为 ,直线
,直线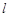 的极坐标方程为
的极坐标方程为 ,且点A在直线
,且点A在直线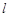 上.
上.
(Ⅰ)求 的值及直线
的值及直线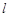 的直角坐标方程;
的直角坐标方程;
(Ⅱ)圆C的参数方程为 ,试判断直线l与圆C的位置关系.
,试判断直线l与圆C的位置关系.
选修4—2:矩阵与变换
已知矩阵 的逆矩阵
的逆矩阵 .
.
(Ⅰ)求矩阵 ;
;
(Ⅱ)求矩阵 的特征值以及属于每个特征值的一个特征向量.
的特征值以及属于每个特征值的一个特征向量.
已知函数f(x)=ex+ax2-ex,a∈R.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求函数f(x)的单调区间;
(Ⅱ)试确定a的取值范围,使得曲线y=f(x)上存在唯一的点P,曲线在该点处的切线与曲线只有一个公共点P.