已知首项为
的等比数列
的前
项和为
, 且
成等差数列.
(Ⅰ) 求数列
的通项公式;
(Ⅱ) 证明
.
如图,在正方体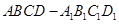 中,
中,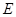 是
是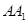 的中点.
的中点.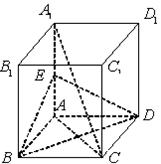
(1)求证: 平面
平面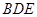 ;
;
(2)求证:平面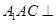 平面
平面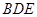 ;
;
(3)求直线BE与平面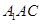 所成角的正弦值.
所成角的正弦值.
在△ABC中,角A,B,C所对边长分别为a,b,c,且c=3,C=60°
(1)若a=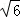 ,求角A;(2)若
,求角A;(2)若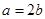 ,求△ABC的面积.
,求△ABC的面积.
如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)
(1)试说出该几何体是什么几何体;
(2)按实际尺寸画出该几何体的直观图,并求它的表面积及体积.(只要做出图形,不要求写作法)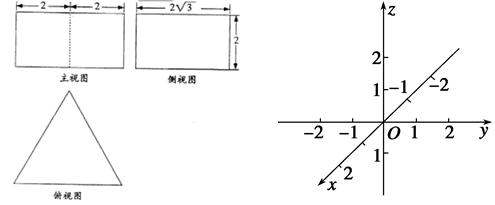
(1) 求不等式的解集: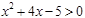
(2)已知三角形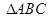 的三个顶点是
的三个顶点是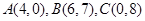 求
求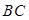 边上的高所在直线的方程;
边上的高所在直线的方程;
已知函数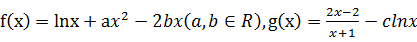 .
.
(1当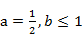 时,
时, 与
与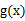 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的 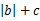 的最小值。
的最小值。
(2)当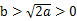 时,求证:存在
时,求证:存在 ,使
,使 的三个不同的实数解
的三个不同的实数解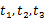 ,且对任意
,且对任意 且
且 都有
都有 .
.