如图,已知三棱锥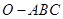 的侧棱
的侧棱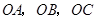 两两垂直,且
两两垂直,且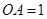 ,
, ,
, 是
是 的中点.
的中点.
(1)求异面直线 与
与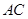 所成的角的余弦值
所成的角的余弦值
(2)求二面角 的余弦值
的余弦值
(3) 点到面
点到面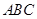 的距离
的距离
(本题12分)
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数ξ的分布列及数学期望Eξ.
(本题12分)
已知函数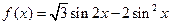 .求:
.求:
(1)求函数 的最大值; (2)求函数
的最大值; (2)求函数 的单调增区间。
的单调增区间。
设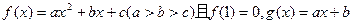
(1)求证:函数y=f(x)与y=g(x)的图像有两个交点;
(2)设f(x)与g(x)的图像交点A、B在x轴上的射影为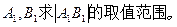
已知向量 =(3,-4)
=(3,-4)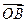 =(6,-3)
=(6,-3)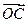 =(5-m, -3-m)
=(5-m, -3-m)
(1)若点A、B、C不能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,求实数m的值。
如图在△ABC中,H为垂心BH·BC=6又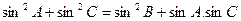
(1)求B的大小;
(2)求△ABC的面积。