在如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.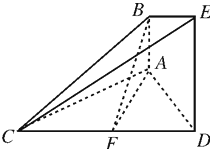
(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE.
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为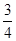 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为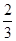 ,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(1)求该射手恰好命中两次的概率;
(2)求该射手的总得分X的分布列及数学期望E(X);
(3)求该射手向甲靶射击比向乙靶射击多击中一次的概率.
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数字-1,0,1,2.称“从盒中随机抽取一张,记下卡片上的数字后并放回”为一次试验(设每次试验的结果互不影响).
(1)在一次试验中,求卡片上的数字为正数的概率;
(2)在四次试验中,求至少有两次卡片上的数字都为正数的概率;
(3)在两次试验中,记卡片上的数字分别为X,η,试求随机变量X=X·η的分布列与数学期望E(X).
某次考试中,从甲,乙两个班各抽取10名学生的成绩进行统计分析,两班10名学生成绩的茎叶图如图所示,成绩不小于90分为及格.
(1)从每班抽取的学生中各抽取一人,求至少有一个及格的概率;
(2)从甲班10人中取两人,乙班10人中取一人,三人中及格人数记为X,求X的分布列和数学期望.
某学生参加某高校的自主招生考试,须依次参加A,B,C,D,E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试.已知每一项测试都是相互独立的,该生参加A,B,C,D四项考试不合格的概率均为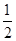 ,参加第五项不合格的概率为
,参加第五项不合格的概率为 .
.
(1)求该生被录取的概率;
(2)记该生参加考试的项数为X,求X的分布列和期望.
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜3次,每次相互独立;
②每次竞猜时,先由甲写出一个数字,记为a,再由乙猜甲写的数字,记为b,已知a,b∈{0,1,2,3,4,5},若|a-b|≤1,则本次竞猜成功;
③在3次竞猜中,至少有2次竞猜成功,则两人获奖.
求甲乙两人玩此游戏获奖的概率.