下图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的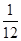 ,
,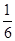 ,
, ,
,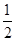 .游戏规则如下:
.游戏规则如下: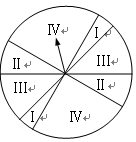
① 当指针指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分;
② (ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束;
(ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积分不高于40分,则最终积分为0分,否则最终积分为100分,游戏结束.
设某人参加该游戏一次所获积分为 .
.
(1)求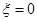 的概率;
的概率;
(2)求 的概率分布及数学期望.
的概率分布及数学期望.
已知函数 .
.
(1)求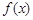 的最小正周期;
的最小正周期;
(2)求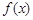 的的最大值和最小值;
的的最大值和最小值;
(3)若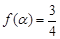 ,求
,求 的值.
的值.
在等比数列 中,
中,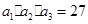 ,
,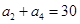 ,
,
试求:(1)首项 和公比
和公比 ;(2)前6项的和
;(2)前6项的和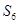 .
.
(本小题满分12分)如图,直三棱柱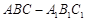 中,
中, ,
,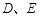 分别为
分别为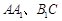 的中点,
的中点,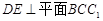 ,二面角
,二面角 的大小为
的大小为 .
.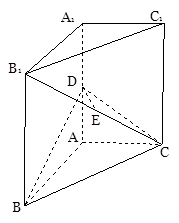
(Ⅰ)证明: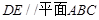 ;
;
(Ⅱ)求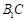 与平面
与平面 所成的角的大小.
所成的角的大小.
(本小题满分12分)甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为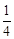 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为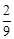 .
.
(Ⅰ)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(Ⅱ)若让每台机床各自加工2个零件(共计6个零件),求恰好有3个零件是一等品的概率.
(本小题满分12分)如图,在三棱锥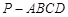 中 ,
中 ,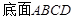 为正方形,
为正方形, ,
,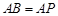 ,
,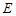 为
为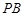 的中点.
的中点.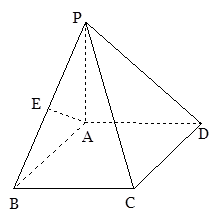
(Ⅰ)证明: ;
;
(Ⅱ)求二面角 的大小.
的大小.