某市为准备参加省中学生运动会,对本市甲、乙两个田径队的所有跳高运动员进行了测试,用茎叶图表示出甲、乙两队运动员本次测试的跳高成绩(单位:cm,且均为整数),同时对全体运动员的成绩绘制了频率分布直方图.跳高成绩在185cm以上(包括185cm)定义为“优秀”,由于某些原因,茎叶图中乙队的部分数据丢失,但已知所有运动员中成绩在190cm以上(包括190cm)的只有两个人,且均在甲队. 
(Ⅰ)求甲、乙两队运动员的总人数a及乙队中成绩在[160,170)(单位:cm)内的运动员人数b;
(Ⅱ)在甲、乙两队所有成绩在180cm以上的运动员中随机选取2人,已知至少有1人成绩为“优秀”,求两人成绩均“优秀”的概率;
(Ⅲ)在甲、乙两队中所有的成绩为“优秀”的运动员中随机选取2人参加省中学生运动会正式比赛,求所选取运动员中来自甲队的人数X的分布列及期望.
(本小题满分12分)双曲线 的离心率为
的离心率为 ,右准线为
,右准线为 。
。
(Ⅰ)求双曲线C的方程;
(Ⅱ)已知直线 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆 上,求m的值.
上,求m的值.
(本小题满分12分)(文)设函数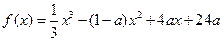 ,其中常数a>1
,其中常数a>1
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若当x≥0时,f(x)>0恒成立,求a的取值范围。2
21、(理)已知 是函数
是函数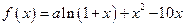 的一个极值点。
的一个极值点。
(Ⅰ)求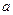 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(本小题满分12分)如图,直三棱柱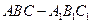 中,AB=1,
中,AB=1, ,∠ABC=60
,∠ABC=60 .
.
(Ⅰ)证明: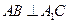 ;
;
(Ⅱ)求二面角A— —B的大小。
—B的大小。
(理)数列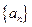 的前
的前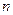 项和记为
项和记为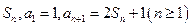
(Ⅰ)求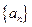 的通项公式;
的通项公式;
(Ⅱ)等差数列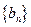 的各项为正,其前
的各项为正,其前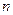 项和为
项和为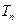 ,且
,且 ,又
,又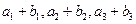 成等比数列,求
成等比数列,求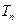
(本小题满分12分)(文)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。
(Ⅰ)求再赛2局结束这次比赛的概率;
(Ⅱ)(文)求甲获得这次比赛胜利的概率。