【提出问题】
（1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．
【类比探究】
（2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．
【拓展延伸】
（3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．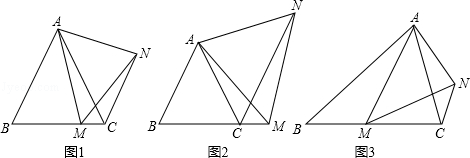
已知：如图△ABC中，∠ACB=90°，点E是边BC上一点，过点E作FE⊥BC（垂足为E）交AB于点F，且EF=AF，以点E为圆心，EC长为半径作⊙E,交BC于点D．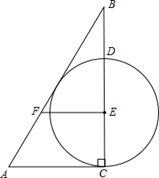
（1）求证：直线AB是⊙E的切线；
（2）设直线AB和⊙E的公共点为G，AC=8，EF=5，连接EG，求⊙E的半径r．
解方程：
（1）如图１，以
的边
、
为边分别向外作正方形
和正方形
，连结
，试判断与
面积之间的关系，并说明理由；
（2）园林小路，曲径通幽，如图２所示，小路由白色的正方形大理石和黑色的三角形大理石铺成．已知中间的所有正方形的面积之和是
平方米，内圈的所有三角形的面积之和是
平方米，这条小路一共占地多少平方米？
如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF＝∠ADF.
（1）求证：△ADE≌△BFE；
（2）连接EG，判断EG与DF的位置关系并说明理由.
如图，∠AOB=30°，OC平分∠AOB，CD⊥OA于D，CE∥AO交OB于E，CE=20cm，求CD的长.