如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm
| 伞架 |
DE |
DF |
AE |
AF |
AB |
AC |
| 长度 |
36 |
36 |
36 |
36 |
86 |
86 |
(1)求AM的长.
(2)当∠BAC=104°时,求AD的长(精确到1cm).
备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.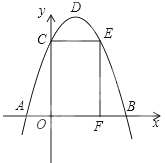
现有一笔直的公路连接M、N两地。甲车从 M 地 驶往 N地,速度为每小时60km;同时乙车从N地驶往M 地,速度为每小时80 km。途中甲车发生故障,于是停车修理了2.5h,修好后立即开车驶往N地。设乙车行驶的时间为t h,两车之间的距离为S km。已知 S与 t 的函数关系的部分图像如图所示。
(1)求出甲车出发几小时后发生故障。
(2)请指出图中线段 BC 的实际意义;
(3)将S与 t 的函数图像补充完整(需在图中标出相应的数据)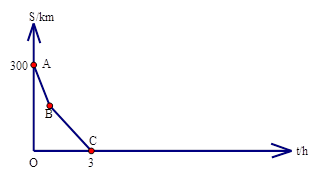
如图,A市在B市的北偏东60°方向,在C市的西北方向,D市在B市的正南方向.已知A、B两市相距120km,B、D两市相距100 km..问:A市与C、D两市分别相距多少千米?(结果精确到1 km)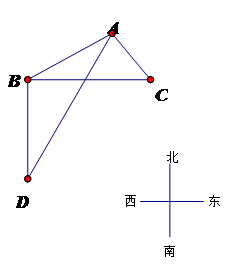
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下: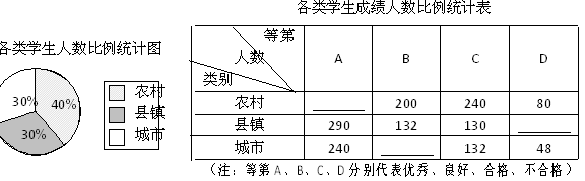
(1)请将上面表格中缺少的三个数据补充完整;
(2)若该市九年级共有60 000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.
小明与甲、乙两人一起玩“手心手背”的游戏.他们约定:如果三人中仅有一人出“手心”或“手背”,则这个人获胜;如果三人都出“手心”或“手背”,则不分胜负,那么在一个回合中,如果小明出“手心”,则他获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)