如图,直线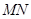 交圆
交圆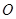 于
于 两点,
两点,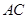 是直径,
是直径,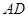 平分
平分 ,交圆
,交圆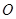 于点
于点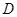 , 过
, 过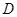 作
作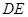 丄
丄 于
于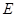 .
.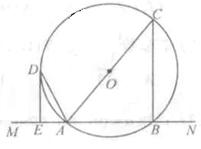
(1)求证: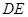 是圆
是圆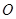 的切线;
的切线;
(2)若 ,求
,求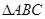 的面积
的面积
(本小题满分12分)设函数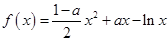 (
( ).
).
(1)当 时,讨论函数
时,讨论函数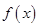 的单调性;
的单调性;
(2)若对任意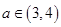 及任意
及任意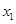 ,
,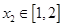 ,恒有
,恒有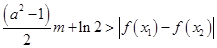 成立,求实数
成立,求实数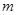 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆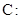
 (
(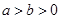 )的离心率为
)的离心率为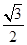 ,
,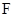 是椭圆的焦点,点
是椭圆的焦点,点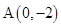 ,直线
,直线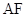 的斜率为
的斜率为 ,
, 为坐标原点.
为坐标原点.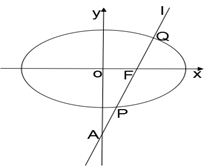
(1)求椭圆 的方程;
的方程;
(2)设过点 的直线与
的直线与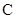 相交于
相交于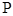 、
、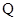 两点,当
两点,当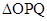 的面积最大时,求
的面积最大时,求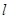 的方程.
的方程.
(本小题满分12分)为了响应学校“学科文化节”活动,数学组举办了一场数学知识竞赛,共分为甲、乙两组.其中甲组得满分的有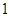 个女生和
个女生和 个男生,乙组得满分的有
个男生,乙组得满分的有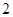 个女生和
个女生和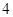 个男生.现从得满分的学生中,每组各任选
个男生.现从得满分的学生中,每组各任选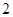 个学生,作为数学组的活动代言人.
个学生,作为数学组的活动代言人.
(1)求选出的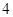 个学生中恰有
个学生中恰有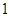 个女生的概率;
个女生的概率;
(2)设 为选出的
为选出的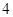 个学生中女生的人数,求
个学生中女生的人数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知三棱柱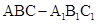 中,侧棱垂直于底面,
中,侧棱垂直于底面,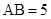 ,
,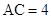 ,
,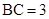 ,
,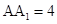 ,点
,点 在
在 上.
上.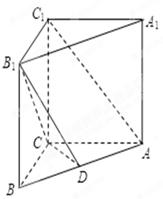
(1)若 是
是 中点,求证:
中点,求证: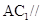 平面
平面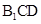 ;
;
(2)当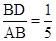 时,求二面角
时,求二面角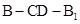 的余弦值.
的余弦值.
(本小题满分12分)已知数列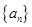 是公差不为
是公差不为 的等差数列,
的等差数列,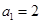 ,且
,且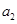 ,
,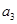 ,
,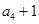 成等比数列.
成等比数列.
(1)求数列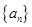 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列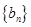 的前
的前 项和
项和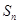 .
.