甲乙两队参加知识竞赛，每队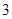
人，每人回答一个问题，答对者为本队赢得一分，答错得零分。假设甲队中每人答对的概率均为
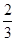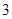，乙队中人答对的概率分别为
且各人正确与否相互之间没有影响.用
表示甲队的总得分.
（Ⅰ）求随机变量分布列
（Ⅱ）用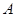
表示“甲、乙两个队总得分之和等于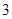”这一事件，用
表示“甲队总得分大于乙队总得分”这一事件，求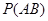
。
（本小题满分12分）设函数
。（Ⅰ）求函数
的最小正周期；（Ⅱ）若函数
的图像与函数
的图像关于原点对称，求
的值。
在直角坐标系xoy中，以o为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为
，M,N分别为C与x轴，y轴的交点
（1）写出C的直角坐标方程，并求出M,N的极坐标；
（2）设MN的中点为P，求直线OP的极坐标方程.
设函数
．
（1）解不等式
；
（2）若关于的不等式
的解集不是空集，试求
的取值范围．
（本小题满分10分）
如图，⊙O内切于△ABC的边于D，E，F，AB=AC，连接AD交⊙O于点H，直线HF交BC的延长线于点G。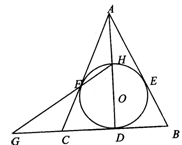
（1）求证：圆心O在直线AD上；
（2）求证：点C是线段GD的中点。
（本小题满分12分）
设函数
，其中
表示不超过
的最大整数，如
.
（1）求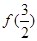
的值；
（2）若在区间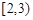
上存在x，使得
成立，求实数k的取值范围；
（3）求函数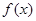
的值域.