“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| |
男性 |
女性 |
合计 |
| 反感 |
10 |
|
|
| 不反感 |
|
8 |
|
| 合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是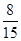 .
.
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
| P(K2>k) |
0.05 |
0.025 |
0.010 |
0.005 |
| k |
3.841 |
5.024 |
6.635 |
7.879 |
下面的临界值表供参考:
(参考公式:K2=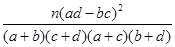 ,其中n="a+b+c+d)"
,其中n="a+b+c+d)"
(本小题满分12分)
已知函数
 是偶函数.
是偶函数.
(Ⅰ)求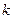 的值;
的值;
(Ⅱ)设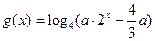 ,若函数
,若函数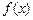 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围.
(本小题满分12分)锐角 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,(Ⅰ)求
,(Ⅰ)求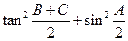 的值;(Ⅱ)若
的值;(Ⅱ)若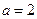 ,
, ,求
,求 的值.
的值.
(本小题满分14分)
现有甲,乙,丙,丁四名篮球运动员进行传球训练,由甲开始传球(即第一次传球是由甲传向乙或丙或丁),记第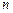 次传球球传回到甲的不同传球方式种数为
次传球球传回到甲的不同传球方式种数为 .
.
(1)试写出 ,
, 并找出
并找出 与
与 (
( )的关系式;
)的关系式;
(2)求数列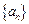 的通项公式;
的通项公式;
(3)证明:当 时,
时, 
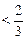 .
.
(本小题满分13分)
(1)若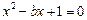 (
( ),试求实数
),试求实数 的范围;
的范围;
(2)设实数 ,函数
,函数 ,
,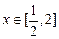
试求函数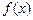 的值域。
的值域。
(本小题满分12分)
已知不等式组 所表示的平面区域为D
所表示的平面区域为D ,记D
,记D 内的整点个数为
内的整点个数为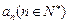 (整点即横坐标和纵坐标均为整数的点).
(整点即横坐标和纵坐标均为整数的点).
(1)数列 的通项
的通项 公式
公式 ;
;
(2)若 ,记
,记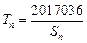 ,求证:
,求证: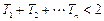 .
.