如图:在多面体EF-ABCD中,四边形ABCD是平行四边形,△EAD为正三角形,且平面EAD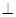 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,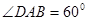 .
.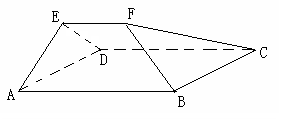
(Ⅰ)求多面体EF-ABCD的体积;
(Ⅱ)求直线BD与平面BCF所成角的大小.
(本小题满分12分)
已知数列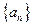 :
: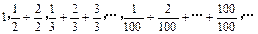
①观察规律,归纳并计算数列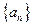 的通项公式,它是个什么数列?
的通项公式,它是个什么数列?
②若 ,设
,设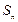 =
= ,求
,求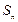 。
。
③设
(本小题满分12分)
已知关于x的二次方程 的两根
的两根 满足
满足 ,且
,且 .(1)试用
.(1)试用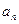 表示
表示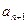 ;(2)求证:数列
;(2)求证:数列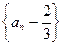 是等比数列;(3)求数列
是等比数列;(3)求数列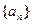 的前n项和
的前n项和 .
.
(本小题满分12分)
己知 三顶点
三顶点 的坐标分别为
的坐标分别为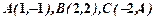 .(1)求
.(1)求 的值;(2)若
的值;(2)若 为
为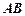 边上的高,求垂足
边上的高,求垂足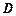 的坐标;(3)求
的坐标;(3)求 的面积.
的面积.
(本小题满分12分)
如图所示,动物园要围成相同面积的长方形虎笼四间,一面可以利用原有的墙,其他各面用钢筋网围成。⑴现有可围36m长钢筋网材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?⑵若使每间虎笼面积为24m2,则每间虎笼的长、宽各设计为多少时,可始围成四间虎笼的钢筋网总长最小?
设 的内角
的内角 的对边分别为
的对边分别为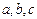 ,且满足
,且满足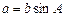 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)求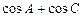 的取值范围.
的取值范围.