(本小题满分12分)
己知 三顶点
三顶点 的坐标分别为
的坐标分别为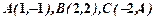 .(1)求
.(1)求 的值;(2)若
的值;(2)若 为
为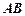 边上的高,求垂足
边上的高,求垂足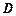 的坐标;(3)求
的坐标;(3)求 的面积.
的面积.
已知函数f(x)=ex-ln(x+m).
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
已知x=3是函数f(x)=aln(1+x)+x2-10x的一个极值点.
(1)求a;
(2)求函数f(x)的单调区间;
(3)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
现有一张长为80 cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块正方形铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x(cm),高为y(cm),体积为V(cm3)
(1)求出x与 y的关系式;
(2)求该铁皮盒体积V的最大值.
设f(x)=a(x-5)2+6ln x,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
已知函数f(x)=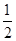 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R.
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)求f(x)的单调区间.